Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Bodová a stejnoměrná konvergence + Lebesgueovy prostory
#1 18. 01. 2021 21:08
Bodová a stejnoměrná konvergence + Lebesgueovy prostory
Mám tento teoretický příklad:
Předpoklady:
Nechť 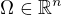 je omezená oblast,
je omezená oblast, 
Nejdříve mám definovat
1)
2)
3)
4)
Pak se mají dokázat implikace, nebo najít protipříklady:
a) 1 → 4
b) 4 → 3
c) 2 → 4
d) 4 → existuje vybraná podposloupnost, tak, že: 
Řešení:
definice:
1) 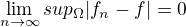
2) 
3) 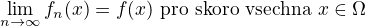
4) 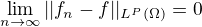
Ale nevím si moc rady s těmi implikacemi (důkaz/protipříklad).
Předem díky za pomoc.
Offline
#2 19. 01. 2021 14:13 — Editoval nejsem_tonda (19. 01. 2021 14:16)
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Bodová a stejnoměrná konvergence + Lebesgueovy prostory
Ahoj,
a) Plati. Rozepis si definici 4 jeste podrobneji a dukaz vymyslis.
b) Hledej protipriklad. Je to "znama" uloha, takze pokud si nebudes delsi dobu vedet rady, zkus prohledat anglicky internet, otevrit skripta apod..
c) Hledej protipriklad. Vem si nejakou funkci, ktera neni integrovatelna (napriklad v [mathjax]L^1(-1;1)[/mathjax]) a zacni si s ni hrat..
d) Plati. Jde o zname lemma, ktere bys mel najit v kazdych skriptech o tomto tematu.
Par poznamek:
a) rika zhruba to, ze stejnomerna konvergence je dost silna.
c) rika, ze bodova konvergence je dost slaba.
b), d) rikaji, ze pri praci s konvergenci v [mathjax]L^p[/mathjax] musime byt opatrni, protoze rychle zavery casto vyzaduji nejake upresneni.
Offline
#3 22. 01. 2021 09:23
Re: Bodová a stejnoměrná konvergence + Lebesgueovy prostory
Dospěl jsem k následujícímu, moc toho není:
a) I → IV
má plynout z věty o záměně limity a integrálu pro stejnoměrnou konvergenci – nevím ale, jak takovou větu formulovat, aby opravdu odpovídala stejnoměrné konvergenci. Jinak předpokládám Levi/Lebesgue v.
b) IV→ III
bodová konvergence nezaručuji konvergenci v Lp (Ω), pro p náležející [1,∞)
protipříklad? moc nerozumím![kopírovat do textarea $\{\chi _{[0,1]},\chi _{[0,1/2]},\chi _{[1/2,1]},\chi _{[0,1/4]},\chi _{[1/4,1/2]},...\}$](/mathtex/94/94c72d1d2c6dc7291f67c82c6352ac15.gif)
Konverguje k triviální funkci v Lp (Ω pro p náležející [1,∞), ale není pravda, že by funkce konvergovala skoro všude
c) II→ IV
f_n (x) =
= 1, pokud x náleží (n, n+1)
= 0, jinak
f_n → 0 na (0, +,∞), ale f_n nekonverguje bodově k nule v Lp (0, +,∞),
neboť 
nekonverguje bodově k nule
d) IV → (f_n,k → f, skoro všude na Ω)
Lp…reflexivní a {f_n} omezená posloupnost,
Posloupnost {f_n} má vybranou podposloupnost {f_n,k} pro všechna L náležející Lp(Ω)* = Lp‘(Ω), 1/p + 1/p´ = 1, pak ale f_n,k → f skoro všude na Ω.
Moc se omlouvám za "neučesanost".
Offline
#4 26. 01. 2021 15:11 — Editoval nejsem_tonda (26. 01. 2021 15:12)
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Bodová a stejnoměrná konvergence + Lebesgueovy prostory
↑ 2M70:
Moc ti nerozumim. Prijde mi, ze by ti pomohlo si to vice promyslet, ale to za tebe nemuze nikdo udelat. To muzes jedine ty sam.
Dospěl jsem k následujícímu...
Dospel jsi k tomu ty, nebo to jsou nejake navody od nekoho jineho? Ono totiz z tech tvych poznamek vubec neni jasne, kterym rozumis a kterym ne.
a) Ja si nazvy tech vet uz moc nepamatuju a skoro jiste pujde nejaka pouzit. Ale neni potreba nic komplikovaneho.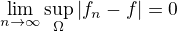 , takze pro libovolne pevne zvolene [mathjax]\varepsilon>0[/mathjax] pro vsechna [mathjax]n[/mathjax] pocinaje od nejakeho cisla plati
, takze pro libovolne pevne zvolene [mathjax]\varepsilon>0[/mathjax] pro vsechna [mathjax]n[/mathjax] pocinaje od nejakeho cisla plati  nebo-li pro vsechna [mathjax]x\in\Omega[/mathjax] plati
nebo-li pro vsechna [mathjax]x\in\Omega[/mathjax] plati  a tedy
a tedy  . Potom se da [mathjax]L^p[/mathjax] norma (pro [mathjax]1\leq p < \infty[/mathjax]) dobre odhadnout:
. Potom se da [mathjax]L^p[/mathjax] norma (pro [mathjax]1\leq p < \infty[/mathjax]) dobre odhadnout: .
.
Diky tomu, ze [mathjax]\Omega[/mathjax] je omezena, tak mame vyhrano. Podrobne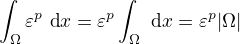 , takze
, takze  pro vsechna [mathjax]n[/mathjax] pocinaje od nejakeho cisla.
pro vsechna [mathjax]n[/mathjax] pocinaje od nejakeho cisla.
Vzhledem k tomu, ze pro kazde (libovolne male) [mathjax]\varepsilon[/mathjax] uvedena nerovnost plati pro vsechna [mathjax]n[/mathjax] pocinaje od nejakeho cisla, dokazali jsme, ze .
.
Pro [mathjax]p=\infty[/mathjax] je [mathjax]L^p[/mathjax] norma definovana trosku jinak. To uz si promysli sam, ktere radky se malicko zmeni.
b) Ano, takovy protipriklad funguje. Pro lepsi porozumeni doporucuju nakreslit si obrazky. Na prvnim obrazku je graf funkce [mathjax]\chi_{[0,1]}[/mathjax], na druhem obrazku graf funkce [mathjax]\chi_{\left[0,\frac12\right]}[/mathjax], na tretim [mathjax]\chi_{\left[\frac12,1\right]}[/mathjax] atd. Potom ti bude jasne, ze pro kazde pevne zvolene [mathjax]a\in [0,1][/mathjax] limita [mathjax]\lim_{n\to\infty}f_n(a)[/mathjax] neexistuje, takze neexistuje ani funkce, ke ktere by posloupnost bodove konvergovala. Pritom [mathjax]L^p[/mathjax] norma funkci [mathjax]f_n[/mathjax] jde v limite k nule.
c) Tady jsi nesplnil, aby [mathjax]\Omega[/mathjax] byla omezena, jinak tvuj priklad funguje. No ale staci si vzit napriklad funkci [mathjax]g(x)=\frac{1}{x^2}[/mathjax], ktera rozhodne nema konecnou [mathjax]L^p[/mathjax] normu pro zadne [mathjax]1\leq p \leq\infty[/mathjax] na [mathjax]\Omega=[-1,1][/mathjax]. Funkce [mathjax]f_n[/mathjax] si definujeme treba jako [mathjax]f_n(x)=\frac{1}{nx^2}[/mathjax]. Je jasne, ze pro zvolene [mathjax]n[/mathjax] nema ani funkce [mathjax]f_n[/mathjax] konecnou normu, ale pritom pro pevne zvolene [mathjax]a\in[-1,1][/mathjax] plati [mathjax]\lim_{n\to\infty}f_n(a)=\lim_{n\to\infty}\frac{1}{na^2}=0[/mathjax], takze funkce [mathjax]f_n[/mathjax] maji bodovou limitu funkci, ktera je vsude rovna nule.
d) Tady sis asi nasel nejake jeste o trosku obecnejsi lemma, ktere plati pro jakekoliv reflexivni prostory (mezi ktere prostory [mathjax]L^p[/mathjax] taky patri). Prijde mi jako kdybys to opisoval z nejakych poznamek, protoze ta cast "pro vsechna L nalezici" nejak nedava smysl. Otevri skripta nebo internet, pokud stojis o poradnou formulaci.
Offline
#5 31. 01. 2021 13:08
Re: Bodová a stejnoměrná konvergence + Lebesgueovy prostory
↑ nejsem_tonda:
Díky za pomoc, hodně mi to pomohlo. Přiznávám bez mučení, že mi s tím někdo jiný pomáhal, odtud ta neuspořádanost. Omlouvám se za opožděnou odpověď.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Bodová a stejnoměrná konvergence + Lebesgueovy prostory