Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 24. 01. 2021 20:17
Limita fce - ln, dominanční řada
https://ibb.co/LgcZ9Qj
Ahoj, prosím o pomoc při počítání limit funkcí. V tomto semestru se v podstatě věnujeme jen limitám posloupností a fcí, ale při počítání některých příkladů mám pár nejasností. Proč po vytknutí (zvýrazněno) jde závorka k 1, neboli ten zlomek v závorce k 0? V příkladech běžně využíváme zejména dominance, ekvivalence atp., ale když jde tady limita k vlastnímu bodu, jde ta dominance taky použít? Moc ji tam nevidím. Děkuji za pomoc.
Offline
#3 24. 01. 2021 21:51
- david_svec
- Příspěvky: 435
- Pozice: student
- Reputace: 13
Re: Limita fce - ln, dominanční řada
Zdravím,
čitatel zlomku: [mathjax2]\ln \bigg(\frac{2}{\sqrt{1+x^{2}}+\sqrt{1-x^{2}}}\bigg)[/mathjax2] jde ve skutečnosti k nule, když [mathjax]x\to 0[/mathjax]. Jen aby nedošlo ke zmatení. Na výsledek to nemá vliv samozřejmě.
Offline
#4 24. 01. 2021 22:19 — Editoval vlado_bb (24. 01. 2021 22:20)
Re: Limita fce - ln, dominanční řada
↑ david_svec: Ano, mas pravdu, dakujem. Prehliadol som logaritmus.
Offline
#5 24. 01. 2021 22:27
Re: Limita fce - ln, dominanční řada
↑ david_svec:
↑ vlado_bb:
Jasně, děkuji.
Ještě se rovnou zeptám na toto, pokud nevadí:
https://ibb.co/0Z9BppP
Platí pro minus nekonečno opačná dominanční řada než pro plus nekonečno? Vyučující to s námi řešil pro posloupnosti a sdělil, že pro fce je to stejné pro nekonečno, což je jasné, ale platí to samé opačně pro minus nekočno? Jakože q^x je dominantní vůči x^q a to je dominantní vůči lnx, tudíž pro minus nekonečno přesně naopak?
Tady v příkladu se pro minus nekonečno vytkne dominantní člen 3^(x-1), nebo to takto brát nemůžu?
Děkuji.
Offline
#8 25. 01. 2021 16:40
Re: Limita fce - ln, dominanční řada
↑ laszky:
https://ibb.co/XWSBnSb
Prosím, proč tady vytýkáme to 2^x, je to tedy ta „opačná dominance" než pro nekonečno? Jinak bych nechápala, proč ten zlomek v závorce jde k nule, když čitatel i jmenovatel jdou k nule.
Děkuji za objasnění.
Offline


 , menovateľ
, menovateľ 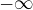 . Stačí takéto odovodnenie ?
. Stačí takéto odovodnenie ?