Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 02. 2021 14:04
Topologie
Dobrý den,
dostalo se mi do ruky následující tvrzení a nemůžu hnout s důkazem. Dokázal by mi, prosím, někdo poradit?
Nechť X je kompaktní Hausdorffův TP. Označme jako Y množinu všech kompaktních neprázdných podmnožin X.
Na Y definujme topologii tak, že její subbáze je tvořena všemi množinami tvaru
[mathjax]\Gamma (U) := \{K\in Y: K \subseteq U\},
[/mathjax]
[mathjax]
\Lambda(V) := \{K\in Y: K\cap V \neq\emptyset\},
[/mathjax]
pro U, V otevřené v X.
Potom
(a) Y je topologický prostor, který je kompaktní a Hausdorffův;
(b) existuje vnoření X do Y.
Offline
#2 16. 02. 2021 20:32 — Editoval Brano (16. 02. 2021 21:16)
Re: Topologie
Hausdorffovost:
Nech  su rozne kompaktne podmnoziny
su rozne kompaktne podmnoziny  . Potom existuje
. Potom existuje  alebo
alebo 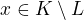 . Bez ujmy na vseobecnosti predpokladajme prvu moznost.
. Bez ujmy na vseobecnosti predpokladajme prvu moznost.
Vsimni si, ze  je regularny, teda existuje otvorena
je regularny, teda existuje otvorena  taka, ze
taka, ze 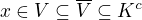 .
.
Over, ze 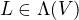 ,
, 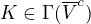 ,
, 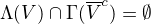 .
.
Kompaktnost: Pouzijeme Alexandrovu vetu o subbaze. Teda chceme dokazat, ze z kazdeho subbazoveho pokrytia  sa da vybrat konecne podpokrytie.
sa da vybrat konecne podpokrytie.
Nech 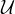 je otvorene pokrytie
je otvorene pokrytie  pomocou prvkov subbazy. Nech
pomocou prvkov subbazy. Nech 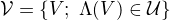 a
a 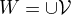 . Potom
. Potom  je otvorena a
je otvorena a 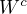 je kompaktna. Ak
je kompaktna. Ak 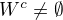 , tak
, tak 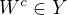 , cize exisuje otvorene
, cize exisuje otvorene  take, ze
take, ze 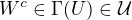 . (Rozmysli si preco a tiez si potom rozmysli specialny pripad, ked
. (Rozmysli si preco a tiez si potom rozmysli specialny pripad, ked 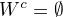 .) Mnozina
.) Mnozina 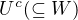 je kompaktna, teda sa da pokryt konecne vela prvkami z
je kompaktna, teda sa da pokryt konecne vela prvkami z  , povedzme
, povedzme 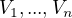 .
.
System 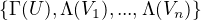 je konecne podpokrytie
je konecne podpokrytie 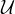 .
.
Vnorenie:
Funkcia 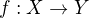 dana
dana 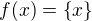 ma pozadovane vlastnosti, over. Potrebujes overit, ze topologia co sa indukuje na jednoprvkove podmnoziny je homeomorfna s povodnou.
ma pozadovane vlastnosti, over. Potrebujes overit, ze topologia co sa indukuje na jednoprvkove podmnoziny je homeomorfna s povodnou.
Offline
