Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 21. 02. 2021 17:44
- Mirek2
- Příspěvky: 1195
Re: Slovní úloha o rychlosti
Návod v otázkách :)
Kolikrát má druhý chodec větší rychlost než první?
Kolikrát větší dráhu ujde za stejnou dobu?
Pak bych si vyznačil úsečku a na ní místo setkání.
Jak dlouho půjde první chodec, než dojde k místu setkání?
Offline
#7 21. 02. 2021 18:33
- marnes

- Příspěvky: 11227
Re: Slovní úloha o rychlosti
↑ anterii:
Na kolik dílů jsi rozdělila celkovou dráhu?
Rychlejší těleso urazilo jakou část celkové dráhy?
Stejnou část vezmeš i z jeho celkové doby pohybu.
Jo. A na začátku vás zdravím.
Offline
#8 21. 02. 2021 18:36
- Mirek2
- Příspěvky: 1195
Re: Slovní úloha o rychlosti
↑ anterii:
Nakresli si úsečku délky y a hned za ní úsečku délky 2y.
První vzdálenost ušel první chodec, tu druhou druhý, než se potkali.
Pak si znovu přečti zadání ...
Offline
#9 21. 02. 2021 20:09
- Mirek2
- Příspěvky: 1195
Re: Slovní úloha o rychlosti
↑ anterii:
Nebo jinak: Místo, kde se potkají, leží v 1/3 vzdálenosti mezi oběma místy.
Offline
#11 22. 02. 2021 09:23
- marnes

- Příspěvky: 11227
Re: Slovní úloha o rychlosti
↑ anterii:
Ale to byl postup. Proč by na všechno musel být vzoreček.
Jo. A na začátku vás zdravím.
Offline
#12 22. 02. 2021 10:05 — Editoval Cheop (24. 02. 2021 09:02)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Slovní úloha o rychlosti
↑ anterii:
Snad nějak takto (pomocí rovnic)
v_1 - rychlost prvního chodce
v_2 - rychlost druhého chodce
čas prvního chodce - t_1 = 3 hodiny
čas druhého chodce - t_2 = 1,5 hodiny
s - celková dráha
t - čas, za který se potkají (máme určit)
Rovnice:
1) [mathjax]s=3v_1[/mathjax]
2) [mathjax]s=1,5v_2[/mathjax]
3) [mathjax]3v_1=1,5v_2[/mathjax]
4) [mathjax]v_2=2v_1[/mathjax]
Dále platí:
5) [mathjax]s=(v_1+v_2)t[/mathjax]
6) [mathjax]s=3v_1\cdot t [/mathjax]
7) [mathjax]t=\frac{s}{3v_1}[/mathjax]
Z rovnice 1 a 7 dostaneme: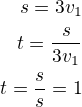
Potkají se za 1 hodinu.
PS: Obecně: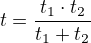
Nikdo není dokonalý
Offline
