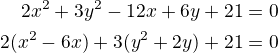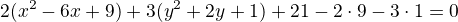Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 05. 2021 21:08 — Editoval osqqi (02. 05. 2021 21:09)
Rovnice elipsy se rovná souřadnicím bodu.
Zdravím, mám příklad [mathjax]2x^2+3y^2-12x+6y+21=0[/mathjax] a mám určit, jedná-li se o rovnici elipsy, nebo ne.
Pokud si to dám do grafického kalkulačky, ukáže se mi, že se jedná o bod. Bohužel však nevím, jak to dokázat.
Předem díky za případnou pomoc.
Offline
#4 03. 05. 2021 08:54
Re: Rovnice elipsy se rovná souřadnicím bodu.
Rovnica ktorú máš ty, je všeobecný tvar rovnice, ktorá môže (ale nemusí) byť rovnicou kuželosečky. Či to tak je, zistíš najlepšie tak že tú rovnicu v obecnom tvare upravíš (alebo sa pokúsiš upraviť) na stredový tvar a stredový tvar rovnice elipsy je: [mathjax]\frac {(x-m)^2}{a^2}+\frac {(y-n)^2}{b^2}=1[/mathjax]. Doplníš výrazy [mathjax]x^2\ldots [/mathjax] a [mathjax]y^2\ldots [/mathjax] na štvorec a hneď uvidíš, že ide o bod. ;)
Offline
#6 03. 05. 2021 10:06 — Editoval Ferdish (03. 05. 2021 10:41) Příspěvek uživatele Ferdish byl skryt uživatelem Ferdish. Důvod: niektorým ľuďom skrátka nevysvetlíš...
#7 04. 05. 2021 16:50
Re: Rovnice elipsy se rovná souřadnicím bodu.
↑ Ferdish:
Vaše chování je s prominutím nevhodné a není potřeba hned někoho urážet. Počítal jsem to, každopádně jsem k výsledku nedošel, proto jsem napsal sem.
Offline
#8 04. 05. 2021 16:58 — Editoval osqqi (04. 05. 2021 17:04)
Re: Rovnice elipsy se rovná souřadnicím bodu.
Cheop napsal(a):
↑ osqqi:
Malé popostrčení:
Mockrát děkuji za slušnou odpověď. K tomuto jsem se dostal, další kroky pak byly tyto:
[mathjax]2(x^2-6x+3)+3(y^2+2y+1)+21=0[/mathjax]
[mathjax]2(x-3)^2-6+3(y+1)^2-1+21=0[/mathjax]
[mathjax]2(x-3)^2+3(y+1)^2=-14[/mathjax]
[mathjax]\frac{2(x-3)^2}{-14}+\frac{3(y+1)^2}{-14}=1[/mathjax]
[mathjax]\frac{-(x-3)^2}{7}+\frac{-3(y+1)^2}{14}=1[/mathjax]
[mathjax]\frac{(3-x)^2}{7}+\frac{(-3-3y)^2}{14}=1[/mathjax]
Dále však nevím, jak dokázat, že se jedná o bod a ne o elipsu.
Offline