Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Pythagoras-ova rovnica
#1 21. 05. 2021 20:21 — Editoval vanok (25. 05. 2021 17:02)
Pythagoras-ova rovnica
Tato tema je pokus odpovede kolegovy ↑↑ MichalAld: na tuto otazku:
Mě by pro začátek stačilo, kdybych pochopil, jak se řeší ty rovnice typu
Tak budem hladat jej nenulove riesenia v mnozine nenulovych celych cisiel. ( to sa da aj vyjadrit takto: budem hladat take riesenia x, y, z danej rovnice, ze
Dam tu dve ( jednoduche ) riesenia danej rovnice.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 25. 05. 2021 18:25
Re: Pythagoras-ova rovnica
Pozdravujem ↑ MichalAld:.
Prva metoda.
Mozeme toto riesenie rozdelit na tri etapy.
A: staci vyriesit problem, pre cele cisla x,y,z ktore su navzajom nesudelitelne.
B: uvazujme (x,y,z) je riesenie, kde x,y,z su navzajom nesudelitelne, tak
a) x, y nemozu byt naraz parne
b) x,y nemozu byt naraz neparne
c) ak predpokladame, ze x je neparne a y parne, tak existuje 2 cele cisla nesudelitelne u a v take, ze x=u-v a y=u+v ktore su stvorce, alebo minus stvorce ( napr. 9 alebo -9 ).
Vyuzite to na urcenie riesenia (x,y,z) ( navzajom nesudelitelne) danej rovnice z #1, take, ze x neparne a y parne.
C: vyuzite A a B na urcenie vsetkych celych rieseni danej rovnice.
A teraz treba vsetko, co je vyssie, podrobne dokazat.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 25. 05. 2021 22:20
Re: Pythagoras-ova rovnica
Ahoj ↑ Honzc:,
Navrh riesenia da riesenie celeho problemu.
Najprv ho ukoncim.
Potom mozes aj ty dat komplrtne riesenie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 25. 05. 2021 22:34
Re: Pythagoras-ova rovnica
Tak teraz riesenie casti A z #2
Si (x,y,z) je cele riesenie rivnice z #1.
Staci delit kazde cislo x,y,z ich najvzädcim spolocnym delitelom d.
Potom (x/d, y/d, z/d) je tiez riesene rovnice rovnice z #1 ( a tieto cidla su navzajom nesudelitelne).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 25. 05. 2021 22:48 — Editoval vanok (26. 05. 2021 11:20)
Re: Pythagoras-ova rovnica
Tu teraz dam riesenie cadti B.
a) tu sa da urobit dokaz sporom.
Predokladam, ze (x,y,z) je riesenie rovninice
Ak x a y su parne tak aj  aj
aj 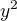 su parne a tak aj
su parne a tak aj 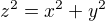 je parne a tak aj
je parne a tak aj  je parne.
je parne.
A to je spor, z prepokladom ze x,y, z du nesudelitelne.
To dokazuje a).
b) na pokracovanie…….
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 26. 05. 2021 13:40
- Richard Tuček

- Místo: Liberec
- Příspěvky: 1206
- Reputace: 19
- Web
Re: Pythagoras-ova rovnica
Nalézt tzv. Pythagorejská čísla lze také takto:
Zvolme si čísla a,b
Položme: x=2ab; y=abs(a^2 - b^2); z=a^2 + b^2
a máme Pyth. čísla.
Offline
#9 26. 05. 2021 19:10
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: Pythagoras-ova rovnica
↑ Richard Tuček:
Ahoj, je ovšem potřeba dokázat, že tímto postupem sestrojíme všechna.
"Máte úhel beta." "No to nemám."
Offline
#11 27. 05. 2021 00:39 — Editoval vanok (27. 05. 2021 01:36)
Re: Pythagoras-ova rovnica
Pozdravujem ↑ MichalAld:,
Co pises, je dobra definicia .
To znamena ze tvoj zapis znamena, ze x ( x cele cislo) musi byt nasobok cisla k. Priklad,
A tak to pouzijem tento pojem na dokaz b) z #3.
Stale predpokladam, ze (x,y,z) je riesenie rovnice z ##1.
Ak x, y su neparne , tak cize
A tiez mame, akoze  je parne tak aj
je parne tak aj  je parne, preto
je parne, preto
No vsak (*) a (**) su protikladne, cize taketo x,y,z nemozu byt riesenie rovnice z #1.
c) na pokracovanie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 27. 05. 2021 15:07
Re: Pythagoras-ova rovnica
vanok napsal(a):
Stale predpokladam, ze (x,y,z) je riesenie rovnice z ##1.
Ak x, y su neparne , tak cizea ,a tak a tiez , co nam da (*).
To platí jen pro tenhle případ, nebo nějak obecně?
Jinak rozumím, že když je x,y liché (neparne), tak že
a to samé pro y, takže
a to nemůže být druhá mocnina celého čísla (ať už bude c jakékoliv).
Offline
#13 27. 05. 2021 15:20
Re: Pythagoras-ova rovnica
Ahoj ↑ MichalAld:,
Vyborne.
Ano aj to staci, v takejto situacii, aby si dokazal, ze take x, y ( x,y su tu neparne) nemozu byt riesenie rovnice z #1.
(A vidis, nemusis to ani vyjadrit vdaka pojmu modulo ….)
Cast dokazu c) napisem tu, dufam, dnes vecer.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 27. 05. 2021 17:28
- check_drummer

- Příspěvky: 5171
- Reputace: 106
Re: Pythagoras-ova rovnica
↑ MichalAld:
Ahoj, x=y (mod m) definujeme tak, že m dělí x-y, tj. je to tvrzení nikoli hodnota nějaké funkce.
"Máte úhel beta." "No to nemám."
Offline
#15 27. 05. 2021 22:04 — Editoval vanok (02. 06. 2021 23:06)
Re: Pythagoras-ova rovnica
Tak, teraz, dam tu dokaz z #3 B c).
Ak x je neparne cele cislo a y parne tak z je neparne ( lebo
Akoze tu x a aj z su neparne tak z+x a aj z-x su parne; preto existuju dve cele cisla u,v take ze :
z+x=2u
z-x=2v
Cize
x=u-v
z=u+v .
u,v su nesudelitelne ( inac by prvocislo p by bol ich spolocny delitel, p by delilo
Tiez mam
co da, ze u aj v ( alebo -u a aj -v) su dokonale stvorce.
( podrobnejsie y =2y’ a preto
To da, ze
Zaver:
Z toho vypliva, ze ak (x,y,z) je jedno riesenie rovnice z #1 z x,y,z navzajom nesudelitelne a take, ze x je neparne a y parne, tak existuju dve cele cisla  , nesudelitelne take, ze
, nesudelitelne take, ze
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 30. 05. 2021 00:04 — Editoval vanok (03. 06. 2021 10:29)
Re: Pythagoras-ova rovnica
Riesenie bodu C).
Vdaka predoslym bodom je jasne, ze vseobecne riesenie rovnice z #1 su:
(trivialne riesenia)
a take,ze
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 30. 05. 2021 00:11
Re: Pythagoras-ova rovnica
Druhe riesenie.
Tu budem hladat vsetki rationalne riesenia rovnice
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 03. 06. 2021 20:18 — Editoval vanok (04. 06. 2021 04:15)
Re: Pythagoras-ova rovnica
Tu dam riesenie rovnice z #17, vdaka tymto troch casti:
D) Najprv overme, ze rovnica z#17 vedie k rieseniu rovnice z#1.
Nech  je kruznica rocnice
je kruznica rocnice
A nech  Ma rovnicu
Ma rovnicu
Tato priamka prechadza cez bod suradnic
Bod roviny je racionnalny, ak ma racionnalne suradnice .
E)Najdime aj druhy bod 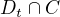 .
.
F) Tu uvazujme kruznicu 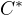 ktorej stred je racionalny bod roviny a takej, ze ma racionalny polomer.
ktorej stred je racionalny bod roviny a takej, ze ma racionalny polomer.
Tiez uvazujme priamku 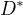 rovnice
rovnice
A odpovedzme na tieto tri otazky
a) ak a,b,c su racionalne, tak druhy bod z
b) dokazte reciprocnu vetu vety a)
c) vdaka a) , b) najdite racionalne riesenia rovnice z#17.
A na koniec
G) vyuzite D), E), F), G) na riesenie rovnice z #1.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 05. 06. 2021 07:33
Re: Pythagoras-ova rovnica
No, minimálně jsem zkoušel, že pro kružnici s racionálním poloměrem, tedy
a přímku, která prochází racionálním bodem kružnice x0, y0 to platit bude, protože přímku
(a když bude racionální x0, y0 bude racionální i to c z rovnice přímky. Naopak to asi neplatí).
No a když to dosadíme do rovnice kružnice, dostaneme
Na začátku jsme předpokládali, že jeden průsečík přímky s kružnici je racionální bod, což je ten x0, y0, takže pro něj platí, že
Takže to nám z rovnice krásně vypadne, a zůstane jen
Z čehož hned plyne, že jeden kořen je t=0, a zůstane už jen lineární rovnice
takže druhé řešení (druhé t) musí být zase racionální, když jsou všechny koeficienty racionální. A tudíž i druhé řešení x1,y1 bude zase racionální.
Ale když na to koukám, tak ve výsledku nevystupuje to r, takže by nemělo záležet na tom, jestli je r racionální nebo né, pokud se nám podaří splnit to
Tedy že stačí aby bylo racionální
Offline
#21 05. 06. 2021 18:44 — Editoval MichalAld (05. 06. 2021 18:45)
Re: Pythagoras-ova rovnica
Zkoušel jsem to ještě i přímo s obecnou rovnicí přímky ... a přijde mi to mnohem složitější, a kdybych nevěděl, co chci aby mi vyšlo, tak bych na to asi nepřišel.
Nicméně, máme kružnici
Potom tedy pro přímku musí platit, že
Teď tedy zkusíme najít ten druhý bod. Rovnici kružnice si trochu upravíme (protože už víme, co nás bude čekat...)
rovnici přímky taky
Poslední úprava je klíčová ... protože až to dosadíme do rovnice kružnice, vznikne tam kupa členů ... a my víme, že x0 má být jeden z kořenů, takže výslednou rovnici by mělo být možné podělit tím kořenem (x-x0). Dále umocníme, ať to můžeme dosadit do kružnice...
a po dosazení dostaneme:
člen
Takto můžeme celou rovnici vykrátit tím kořenem (x-x0), který odpovídá prvním (známému) bodu, a zůstane nám lineární rovnice, která pokud bude mít racionální koeficienty nemůže vytvořit iracionální řešení (nemá tam žádnou odmocninu ani nic jiného, k výsledku se dobereme jen s využitím sčítání, násobení a dělení, což nám iracionální čísla nevytvoří).
Offline
#23 05. 06. 2021 20:40 — Editoval vanok (07. 06. 2021 00:00)
Re: Pythagoras-ova rovnica
Pozdravujem ↑ MichalAld:,
Pred tym, ako dam odpoved na #22, napisem ako predvidane v #18 mozne riesenie na otazky D) a E).
D) mozme predpokladat,
a vtedy je jasne, ze
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#24 05. 06. 2021 21:14 — Editoval vanok (05. 06. 2021 21:47)
Re: Pythagoras-ova rovnica
E) urcime body 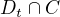 .
.
To nas vedie k rieseniu rovnice
Preto body 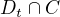 maju suradnice
maju suradnice
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#25 06. 06. 2021 13:48 — Editoval vanok (07. 06. 2021 00:06)
Re: Pythagoras-ova rovnica
F a)
Rovnica kruznice 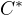 je
je
Tak
Pre
cize
Na dokoncenie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1 2
- Hlavní strana
- » Didaktika a pedagogika: metodiky výuky a výukové materiály
- » Pythagoras-ova rovnica