Matematické Fórum

strixie29 · 08. 06. 2021 08:42

Ahoj, mám úkol do variačních metod. Mám sporem dokázat:

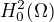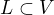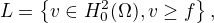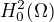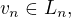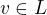Mějme Sobolevův prostor $H^2_0(\Omega)$ a množinu $L\subset V$ takovou že $L=\{v \in H^2_0(\Omega), v\geq f\},$ kde f je spojitá funkce. Chci dokázat, že pokud posloupnost funkcí $v_n \longrightarrow v$ v $H^2_0(\Omega)$ konverguje slabě, $v_n \in L_n,$ pak $v \in L$ . Nevím jak můžete mi pomoct, díky.

Bati · 08. 06. 2021 10:59 — Editoval Bati (08. 06. 2021 11:00)

Ahoj,

zpusob 1) Pouzij funkcional 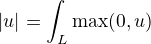$|u|=\int_L\max(0,u)$ a jeho slabou zdola polospojitost.

zpusob 2) Pouzij fakt, ze vsechny uzavrene konvexni mnoziny v tvem prostoru jsou zaroven slabe uzavrene (obecne v jakemkoliv lok. konvexnim TVP).

V pozadi obojiho je Hahn-Banachova veta.

Edit: az ted jsem si vsimnul to "sporem"

Matematické Fórum

#1 08. 06. 2021 08:42

Konvergence

#2 08. 06. 2021 10:59 — Editoval Bati (08. 06. 2021 11:00)

Re: Konvergence

Zápatí