Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prenesenie nerovnosti z kruhov na kompaktnu mnozinu (TOTO TÉMA JE VYŘEŠENÉ)
#1 16. 07. 2021 00:44
Prenesenie nerovnosti z kruhov na kompaktnu mnozinu
Zdravim,
v jednej knizke som videl vetu, kde ide o nerovnicu pre slabe riesenie [mathjax]u[/mathjax] parcialnej diferencialnej rovnice [mathjax]\Delta_p u(x)=h(x)[/mathjax] pre [mathjax]x\in\Omega\subset\mathbb{R}^2[/mathjax], pricom [mathjax]\Omega[/mathjax] je ohranicena mnozina. Nerovnica ktoru treba dokazat je pre Hölderov exponent a ma platit na vsetkych kompaktnych podmnozinach [mathjax]K\subset\Omega[/mathjax].
Na zaciatku dokazu je napisane, ze nerovnost staci dokazat len pre [mathjax]\Omega=B_1[/mathjax] a [mathjax]K=B_{1/4}[/mathjax]. Ale nie je tam uvedeny dovod preco to je dostatocne. A to je moj problem.
Moj napad je, ze [mathjax]K[/mathjax] prekryjem kruhmi ktore sa nachadzaju v [mathjax]\Omega[/mathjax] a potom zmenim mierku tychto kruhov a posuniem ich stred do nuly, cize ich pretransformujem na [mathjax]B_{1/4}[/mathjax]. Nasledne na to dokazem tuto nerovnost pre [mathjax]K=B_{1/4}[/mathjax] a [mathjax]\Omega=B_1[/mathjax]. Potom by som nejako preniesol tuto nerovnost na lubovolnu kompaktnu podmnozinu [mathjax]K\subset\Omega[/mathjax]. Ale zial nemam ziaden logicky argument preco by som to mohol preniest na lubovolne [mathjax]K[/mathjax]. Vedel by to prosim niekto argumentovat?
Offline
- (téma jako vyřešené označil(a) Gauß69)
#3 16. 07. 2021 14:10
Re: Prenesenie nerovnosti z kruhov na kompaktnu mnozinu
↑ Bati:
Ahoj Bati, taketo znenie ma ta veta
Nech [mathjax]\Delta_pu=h[/mathjax] v [mathjax]\Omega [/mathjax] a nech [mathjax]h\in L^q(\Omega )[/mathjax], pricom [mathjax]2<q\leq\infty [/mathjax] a [mathjax]2<p<\infty [/mathjax]. Potom [mathjax]\nabla u \in C^{\beta-1}_\text{loc}(\Omega) [/mathjax]. Okrem toho plati nerovnost pre kazdu kompaktnu podmnozinu [mathjax]K\subset\Omega[/mathjax]:
[mathjax][\nabla u]_{C^{\beta-1}(K)}\leq C(K,p,q,\beta)\cdot \max\left(\|h\|_{L^q(\Omega )}^{\frac{1}{p-1}},\|u\|_{L^\infty(\Omega )}\right)[/mathjax].
Ako som spominal [mathjax]\Omega\subset\mathbb{R}^2 [/mathjax], [mathjax][\nabla u]_{C^{\beta-1}(K)}=\sup\limits_{x,y\in K}\left|\frac{\nabla u(x)-\nabla u(y)}{|x-y|^{\beta-1}}\right|[/mathjax], a [mathjax]\beta[/mathjax] je v zavislosti od [mathjax]p[/mathjax] a [mathjax]q[/mathjax] zadefinovane, vzdy lezi ale v intervale [mathjax][1,2][/mathjax]. Este by som dodal ze [mathjax]\Delta_pu=\text{div}\left(|\nabla u|^{p-2}\nabla u\right)[/mathjax] je [mathjax]p[/mathjax]-Laplace operator, a [mathjax]C^{\beta-1}_\text{loc}(\Omega) [/mathjax] je priestor lokalne Hölder spojitych funkcii.
Offline
#4 18. 07. 2021 12:16
Re: Prenesenie nerovnosti z kruhov na kompaktnu mnozinu
Ahoj ↑ Gauß69:,
ok, to znamena ze ten odhad se tyka reseni p-Laplaceovy rovnice. Vzhledem k tomu, ze se v te rovnici nevyskytuje prostorova promenna x explicitne, mel bys snadno nahlednout ze dukaz toho odhadu projde stejnym zpusobem na 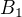 jako na
jako na  . A to zjevne staci na pokryti libovolneho kompaktu.
. A to zjevne staci na pokryti libovolneho kompaktu.
Offline
#5 18. 07. 2021 14:52
Re: Prenesenie nerovnosti z kruhov na kompaktnu mnozinu
↑ Bati:
Vdaka. Cakal som za tym nejaky hlbsi matematicky argument, ale asi to bude ako pises, ze dokaz ide analogovo pre lubovolny kruh v [mathjax]\mathbb{R}^2[/mathjax] a nic ine za tym nebude.
(Este mala poznamka: [mathjax]p[/mathjax]-Laplacova rovnica je len specialny pripad [mathjax]p[/mathjax]-Poissonovej rovnice, ked [mathjax]h\equiv 0[/mathjax].)
Offline
#6 18. 07. 2021 16:08
Re: Prenesenie nerovnosti z kruhov na kompaktnu mnozinu
↑ Gauß69:
Podle me za tim nic vic byt nemuze. Ale kdybys mel nejakou anizotropni rovnici napr. typu ,
,
tak uz ten odhad podle me neudelas (pro kompakty blizko hranice).
(Mas pravdu, ja jen o Poissonove rovnici spis premyslim jako o nehomogenni Laplacove rovnici:)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prenesenie nerovnosti z kruhov na kompaktnu mnozinu (TOTO TÉMA JE VYŘEŠENÉ)
