Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 13. 08. 2021 17:35
- Eratosthenes
- Příspěvky: 3110
- Reputace: 140
Re: Pomoci
↑ Jirka58:
Podívej se na pravidla fóra
https://forum.matweb.cz/misc.php?action=rules
především na
Dobře míněné rady: jak klást dotazy?
Odstavec 3 je přesně o Tobě :-)
Budoucnost patří aluminiu.
Offline
#4 13. 08. 2021 17:45
Re: Pomoci
Díky za zájem. Celé znění příkladu je 10000x^(log^x(x)-5log(x)=1
Nejdříve jsem se to pokoušel celé logaritmovat ale stále jsem narážel na to, že jsem neuměl nějak smysluplně vyjádři to log^x(x).
Poté jsem si uvědomil, že stačí položit (log(x))^x-5log(x)=0 ...stále ale narážím na problém toho vyjádření log^x(x).
Vím, že řešeni je x1=1 a x2=13,6636.....
S pozdravem J
Offline
#7 13. 08. 2021 19:27
#8 16. 08. 2021 17:06
Re: Pomoci
Zdravím,
ještě bych se vrátil k uzávorkování zadání. Pokud má být jedno z řešení x=1, mělo by zadání vypadat nějak takto:
[mathjax](10000x)^{(logx)^{x}-5logx}=1[/mathjax]
Potom je
[mathjax]x_{1}=1[/mathjax]
[mathjax]x_{2}=10^{-5}[/mathjax]
a [mathjax]x_{3}[/mathjax] je řešením rovnice [mathjax]{(logx)^{x}-5logx}=0[/mathjax]. Zatím mě nenapadlo, jak ji vyřešit, takže bych dal přednost :-) zadání
[mathjax](10000x)^{log(x^{x})-5logx}=1[/mathjax]
Hlavní je zápal, talent se dostaví!
Offline
#9 16. 08. 2021 19:47
Re: Pomoci
K tomu řešení jak píšeš x1 = 1 a x2 = 10^(-5) jsem také došel. Pokud však příklad dám do grafu nebo např. do Wolfram Alpha vyjde mi výsledek x3 = 13,6636.....
To x3 prostě zatím nedokážu vypočítat. Je to příklad z maturity z roku asi tak 1890:-)
Offline
#10 18. 08. 2021 03:31
#12 18. 08. 2021 10:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Pomoci
Zdravím,
toto zadání dost koluje po internetu Odkaz, Odkaz, další - stačí zadat k vyhledání např. "thémata písemných zkoušek maturitních 1885". I zde na fóru se objevilo, v závěru odkazovaného tématu jsou celkem užitečné odkazy na zdigitalizované ročenky, mimo jiné i se zadáním maturit. Mám za to, že při archivním bádání jsem narazila i na podrobnější působení c. k. zemského inspektora školního Jana Kosiny.
Zadání je tedy 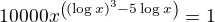 , log bych brala označení pro dekadický a, nemám-li nějakou chybu v úpravě, k řešení po logaritmování bude bikvadratická rovnice, což by absolvent gymnázia měl zvládnout i dnes. Přeji zdar.
, log bych brala označení pro dekadický a, nemám-li nějakou chybu v úpravě, k řešení po logaritmování bude bikvadratická rovnice, což by absolvent gymnázia měl zvládnout i dnes. Přeji zdar.
Offline

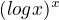 logaritmuješ úplně stejně jako třeba
logaritmuješ úplně stejně jako třeba