Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 08. 2021 14:48 — Editoval tama27 (19. 08. 2021 14:49)
Úhel mezi dvěma vektory
Ahoj, prosím o radu s následujícím příkladem.
Buď 
a 
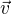vektory takové, že |u| = |v| = 1. Vektory svírají s osou x úhly alfa, respektive beta. Co můžeme říci?
1) V1U1 + V2U2 = cos(beta - alfa)
2) V1U1 + V2U2 = cos(alfa - beta)
3) V2U1 + V1U2 = sin(alfa + beta)
4) V2U1 + V1U2 = sin(alfa - beta)
Můj postup:
Vím, že úhel svíraný mezi vektory (třeba gamma) lze zjistit z vzorce V1U1 + V2U2 = cos(gamma). A gamma = 180 - alfa - beta. Dál ale nevím, jak pokračovat. Moc díky za radu.
Offline
- (téma jako vyřešené označil(a) tama27)
#3 20. 08. 2021 09:25
Re: Úhel mezi dvěma vektory
[mathjax]\gamma = 180-\alpha -\beta [/mathjax]↑ Placka03:
Ahoj, díky za reakci. Vycházím z toho, že úhel mezi vektory je gamma. A protože součet těch tří vektorů musí být 180 (svírají ho s osou x, tedy přímkou), tak 180 = alfa + beta + gamma. Nebo se pletu?
Offline
#4 20. 08. 2021 09:36
Re: Úhel mezi dvěma vektory
↑ tama27:
Zkus si do souřadné soustavy nakreslit dva libovolné vektory [mathjax]\vec{u}, \vec v[/mathjax] jednotkové délky začínající v počátku a vyznač si úhly [mathjax]\alpha, \beta[/mathjax], které oba vektory svírají s osou x. Podívej se, v jakém vztahu jsou s úhlem [mathjax]\gamma[/mathjax] mezi nimi.
Offline
#5 20. 08. 2021 12:42
Re: Úhel mezi dvěma vektory
↑ tama27:
Promiň, špatně jsem tě pochopil. Pokud je zadání myšleno tak, jak to bereš ty, pak podle mě neplatí ani jedna možnost. Spíš bych řekl, že [mathjax]\alpha ,\beta [/mathjax] jsou úhly, které vektory svírají s kladným směrem osy x.
Offline
#6 20. 08. 2021 20:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Úhel mezi dvěma vektory
Zdravím,
téma je sice označeno za vyřešené, ale dovolím si "odoznačít". Některá tvrzení by bylo dobré podrobněji probrat:
tama27 napsal(a):
Vím, že úhel svíraný mezi vektory (třeba gamma) lze zjistit z vzorce V1U1 + V2U2 = cos(gamma).
zde rozumím, že chybí jen upřesnění, že vzorec platí pro speciální podmínku uvedenou v zadání, tj. |u| = |v| = 1
tama27 napsal(a):
[mathjax]\gamma = 180-\alpha -\beta [/mathjax]↑ Placka03:
Ahoj, díky za reakci. Vycházím z toho, že úhel mezi vektory je gamma. A protože součet těch tří vektorů musí být 180 (svírají ho s osou x, tedy přímkou), tak 180 = alfa + beta + gamma. Nebo se pletu?
součet těch tři vektorů (snad jen překlep), tj. součet těch tři úhlů. Je to tak myšleno? Ale čím je dáno, že platí 
?
↑ Placka03: dovolila jsem si obnovit skrytý příspěvek.
Děkuji za upřesnění k tématu.
Offline
#7 20. 08. 2021 21:21
Re: Úhel mezi dvěma vektory
↑ jelena:
Předpokládám, že si autor dotazu představil situaci, kdy první vektor končí v prvním kvadrantu a druhý ve druhém. Potom rovnost [mathjax]\alpha +\beta +\gamma =180^\circ [/mathjax] skutečně platí, pokud uvažujeme nejmenší možné úhly mezi vektory a osou x.
Když ale budeme uvažovat úhly tímto způsobem, neplatí ani jedna z možností. V zadání jsou nejspíš myšleny orientované úhly, které svírá kladný směr osy x a vektory. Potom by platilo [mathjax]\gamma = |\alpha - \beta|[/mathjax], tedy [mathjax]\cos|\alpha - \beta| = u_1 v_1 + u_2 v_2[/mathjax]. Jelikož je kosinus sudá funkce, platí [mathjax]\cos|\alpha - \beta| = \cos(\alpha - \beta) = \cos(\beta-\alpha)[/mathjax], tedy správně jsou možnosti 1 a 2.
Offline
#8 20. 08. 2021 23:06
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: Úhel mezi dvěma vektory
↑ tama27:
V zadání nikde nevidím, že by se mělo jednat o rovinný případ. Lze se to jen oprávněně domnívat z toho, že první dva výrazy jsou zřejmě skalární součin...
Budoucnost patří aluminiu.
Offline
#9 21. 08. 2021 09:16
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Úhel mezi dvěma vektory
Zdravím,
↑ Placka03: děkuji, nepoužití orientovaného úhlu bych se snažila vyvrátit např. tak, že "kolegou zřejmě myšleným postupem", tj. jednou velikosti úhlu (nejmenší odchylky od osy) lze zadat místo jednoho 4 různé vektory. Orientovaný úhel toto vylučuje. Tedy u vektoru se má pracovat s orientovaným úhlem.
↑ Eratosthenes: děkuji, já tam toho nevidím více. Např. zda úloha pokračuje jen zaškrtnutím okénka, se slovem "platí", "neplatí", nebo se očekává podrobné odůvodnění, jak provedl kole ↑ Placka03: v druhém odstavci příspěvku, nebo konverzaci z úlohy "Co můžeme říci?" lze pokračovat "5) V Lážově je krásně za každého počasí".
Metodicky k tomu určitě řeknete více, než já :-) Každopádně autor tématu usekl téma obsahující zřejmé chyby a nedorozumění označením za vyřešené a přidělil kolegovi ↑ Placka03: (za příspěvek 2?) zápornou reputaci.
Minimálně se hodí upřesnění kontextu zadání a použití definic. Děkuji, pozdravy.
Offline