Matematické Fórum

Stary · 20. 11. 2009 10:49

Dva desperáti se rozhodli, že ukončí svůj spor soubojem. Oba dobře ví, že jeden z nich je lepší střelec. První zasáhne a zastřelí svého soupeře s pravděpodobností p1, druhý s pravděpodobností p2. Aby byl souboj vyrovnaný, domluvili se, že budou střílet postupně. Nejprve vystřelí slabší střelec. Pokud mine, bude na řadě druhý střelec. Jestliže i ten mine, bude pokračovat opět první střelec. Souboj pokračuje tak dlouho, dokud nezůstane pouze jeden desperát. Jaké jsou pravděpodobnosti p1 a p2 úspěšné střelby, jestliže víme, že v této hře mají oba desperáti stejnou šanci přežít? Najděte všechna řešení!
Návod: Rozmyslete si pravděpodobnosti výhry po~prvním kole, druém kole, třetím kole a zkuste zobecnit. Využijte znalost součtu geometrické řady.

Jakym zpusobem toto vypocitat???Jak vyuzit soucu geomtricke rady???Diky za radu

jelena · 20. 11. 2009 12:40

↑ Stary:

Zdravím, takový můj pokus - opravdu jen nápad:
p1 - pravděpodobnost, že první zasahne, (1-p1) - pravděpodobnost, že 1. nezasahne (podobně je to pro druhého)

Pravděpodobnost, že maji šanci přežit je 1:1 (tedy výsledná pravděpodobnost jevu P(A) je 0,5)

Začnou střílet:

1. zasahne - konec hry nebo
1. nezasahne a zároveň 2. zasahne - konec hry nebo
1. nesasahne a zároven 2. nezasahne a zároveň 1. zasahne v dalším kole atd.

Z těchto údajů se sestaví zápis pro pravděpodobnost jevu A, zřejmě se v tom musí vykoukat nekonečná geometrická řáda a použit vzorec pro součet nekonečné geometrické řady, součet je 0,5. Hledáme hodnoty p1, p2.

Děkuji za sdělení, zda to má alespoň částečný smysl.

Wotton · 20. 11. 2009 13:49

↑ jelena:

Taky jsem tímhle směrem uvažoval, ale ješte se mi nic z toho nepovedlo sestavit (teda nic co by mi pomohlo).

Jen jeste doplním, že jedno řešení vůbec neuvažuješ, a to že P(A) = P(B) = 0. To je když p1 = p2 = 0. Pak budou střílet do nekonečna:-)

jelena · 20. 11. 2009 13:54

↑ Wotton: nemáji stejnou, neb:

Nejprve vystřelí slabší střelec.

pokud jsem tuto myšlenku správně pochopila.

Wotton · 20. 11. 2009 13:57

↑ jelena:
No je to sporný, dá se to pochpit tak i tak. Rozhodně bych to nepovažoval za plnohodnotný řešení, ale vnitřně musím počítat i s tim.

Stary · 20. 11. 2009 14:05

↑ jelena:

Urcite nemaji stejno vahu (tedy 1:1) protoze jeden z nich je lepsi strelec...Tohle se musi do te rovnice zapracovat ale zatim se mi to jeste nepovedlo...

jelena · 20. 11. 2009 14:11

↑ Stary:

asi jsem nevhodně pochopila tento výraz:

že v této hře mají oba desperáti stejnou šanci přežít

Je to tak?

Pokud nemaji stejnou šanci, pak se sestavi nerovnice "pravděpodobnost, že přežije jeden P(A)" je větší (menší), než pravděpodobnost, že přežije druhý P(B), nebo nerovnice "meniši nebo rovno", pak zapracujeme i sporný bod, zda maji nebo nemaji. Ale 0,5 by se asi objevilo jako hraniční hodnota. Je to tak?

Jev A jsem označila jev, že zvitězí první.

Ostatní také zadání - střelba, přežití - nemohli raděj soutěžit v hodu kostkou?

Wotton · 20. 11. 2009 15:00

Pokud budeme chápat kolo jako dvojici výstřelů a si označíme $Z_n$ že oba žijí po n-tém kole, pak pravděpodobnost že 1. střelí druhého v n+1 kole je $Z_n.p_1$ , a druhý prvního $Z_n.(1-p_1).p_2$

Nyní platí že $P(A)=\sum_{i=0}^{\infty}Z_i.p_1\nl P(B)=\sum_{i=0}^{\infty}Z_i.(1-p_1).p_2$

No a teď už jen úpravama dostaneme: $P(A)=P(B)\nl\sum_{i=0}^{\infty}Z_i.p_1=\sum_{i=0}^{\infty}Z_i.(1-p_1).p_2\nl p_1\sum_{i=0}^{\infty}Z_i=(1-p_1).p_2\sum_{i=0}^{\infty}Z_i\nl p_1=(1-p_1).p_2\nl\frac{p_1}{(1-p_1)}=p_2$

Přičemž nás samozřejmě zajímají jen řesení z intervalu <0,1>. Součet geometrický řady potřebujem jen k tomu, aby jsme ověřili, ze výraz $\sum_{i=0}^{\infty}Z_i$ nenabývá nevlastní hodnoty.

... ale mám dojem, že takhle si to zadávající nepředstavoval:-)

Kondr · 21. 11. 2009 00:58

Koukám že pan učitel dává rád zákeřné navody, nejen tu ale i s tím názvem Trianglie.

Přes geometrickou posloupnost: aby první zastřelil druhého v i-tém kole, musí sám i-1-krát minout, druhý musí také i-krát minout a nakonec se musí první trefit. Dle pravidla součinu je tato pravděpodobnost rovna $P(A_i)=(1-p_1)^{i-1}(1-p_2)^{i-1}\cdot p_1$ . Pravděpodobnost, že první zastřelí druhého je součtem těchto pravděpodobností přes všechna $i$ , tedy $P(A)=\sum_{i=1}^{\infty}P(A_i)=\sum_{i=1}^{\infty}(1-p_1)^{i-1}(1-p_2)^{i-1}\cdot p_1=\sum_{i=0}^{\infty}(1-p_1)^{i}(1-p_2)^{i}\cdot p_1=\frac{p_1}{1-(1-p_1)(1-p2)}$
Naší úlohou je řešit rovnici $0.5=\frac{p_1}{1-(1-p_1)(1-p_2)}$ .

Řešení bez návodu: pravděpodobnost, že vyhraje A nezávisí na tom, kolik kol proběhlo, ale na tom, jestli je na tahu. Označme $P_1$ pravděpodobnost, že A vyhraje, když je na tahu a 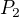$P_2$ pravděpodnost že vyhraje, když na tahu není. Platí
$P_1=p_1+(1-p_1)P_2$ ,
$P_2=(1-p_2)P_1$
sloučením $P_1=p_1+(1-p_1)(1-p_2)P_1$ ,
$P_1=\frac{p_1}{1-(1-p_1)(1-p_2)}$ . A máme to zadarmo.

Stary · 21. 11. 2009 10:22 — Editoval Stary (21. 11. 2009 10:22)

↑ Kondr:
Moc krat ti dekuju za reseni.Jen mi neni jasne kde jsi prisel na to ze dostaneme rovnici $0.5=\frac{p_1}{1-(1-p_1)(1-p_2)}$
konktretne mi neni jasne proc se to rovna 0.5??? Je to proto ze maji kazdy sanci 50% nebo ne??
Dekuji za vysvetleni

jelena · 21. 11. 2009 10:51

↑ Stary:

Zdravím,

teď to bude troufalost nejvyšší - ale troufám si tvrdit, že postup č. 1 váženého Moderátora kolegy Kondra je vysoce kvalitním matematickým zápisem polopatického návodu z příspěvku 2.

Obvykle ještě doplňuji větu "slovo nebo nahrazuji" atd. (můžeš si to ověřit pomocí tlačitka Hledat v horní liště).

------
OT pro kolegu Kondra, pozdrav :-) - v příspěvku Trianglie jsem se snažila naznačit, že z trojuhelníků (což jsou Y- "naruby") se dá poskládat konečný uzavřený graf (nebo jak se tomu odborně říká).

O okolnostech vzniků obou příspěvků někdy jindy - ale byly to okolnosti velmi pozitivní z mého pracovního reálu - tak se teď do něho navratím :-)

petrk · 30. 11. 2009 18:27

Nejsem si zcela jistý proč je tam ta 1/2 . Mohl by mi to někdo prosím vysvětlit?

Kondr · 30. 11. 2009 21:11

↑ petrk:Pokud mají oba desperáti stejnou šanci, má každý šanci 1/2.

petrkovar · 01. 12. 2009 16:59

↑ Kondr: Rád bych věděl, v čem je návod "zákeřný". To jsem v úmyslu neměl. Název trianglie vzešel mj. z obecnější formulace problému.

Kondr · 01. 12. 2009 17:24

↑ petrkovar:Omlouvám se, poněkud jsem to přehnal. Osobně mi připadá rekurzivní řešení hezčí, zejména chceme-li řešit zobecnění úlohy pro n desperátů. Co se týče názvu Trianglie, narážel jsem na Jeleninu poznámku v odkazovaném tématu o duálním grafu, ke které název svádí. Možná přes ni vede cesta, ale řešení zmíňené v návodu s Dirichletovým principem a konečností grafu je (alespoň pro mě) zřejmější.

petrkovar · 01. 12. 2009 17:46

↑ Kondr:Aha! Trianglie je speciální případ "Multianglie" a ne "Polygonalie". Z "three angles" (nebo "tri angles"?) a nikoliv "triangle". Tento příspěvěk ale patří do jiného tématu, že?

Kostja · 05. 12. 2009 16:19 — Editoval Kostja (05. 12. 2009 18:25)

Jenom pro upřesnění

Přes geometrickou posloupnost: aby první zastřelil druhého v i-tém kole, musí sám i-1-krát minout, druhý musí také i-krát minout a nakonec se musí první trefit.

zřejmě jste měl namysli, že druhý musí také i-1-krát minout...

Kondr · 05. 12. 2009 16:37

↑ Kostja:Ano.

Matematické Fórum

#1 20. 11. 2009 10:49

Kombinatorika-slovni uloha

#2 20. 11. 2009 12:40

Re: Kombinatorika-slovni uloha

#3 20. 11. 2009 13:49

Re: Kombinatorika-slovni uloha

#4 20. 11. 2009 13:54

Re: Kombinatorika-slovni uloha

#5 20. 11. 2009 13:57

Re: Kombinatorika-slovni uloha

#6 20. 11. 2009 14:05

Re: Kombinatorika-slovni uloha

#7 20. 11. 2009 14:11

Re: Kombinatorika-slovni uloha

#8 20. 11. 2009 15:00

Re: Kombinatorika-slovni uloha

#9 21. 11. 2009 00:58

Re: Kombinatorika-slovni uloha

#10 21. 11. 2009 10:22 — Editoval Stary (21. 11. 2009 10:22)

Re: Kombinatorika-slovni uloha

#11 21. 11. 2009 10:51

Re: Kombinatorika-slovni uloha

#12 30. 11. 2009 18:27

Re: Kombinatorika-slovni uloha

#13 30. 11. 2009 21:11

Re: Kombinatorika-slovni uloha

#14 01. 12. 2009 16:59

Re: Kombinatorika-slovni uloha

#15 01. 12. 2009 17:24

Re: Kombinatorika-slovni uloha

#16 01. 12. 2009 17:46

Re: Kombinatorika-slovni uloha

#17 05. 12. 2009 16:19 — Editoval Kostja (05. 12. 2009 18:25)

Re: Kombinatorika-slovni uloha

#18 05. 12. 2009 16:37

Re: Kombinatorika-slovni uloha

Zápatí