Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 22. 11. 2009 13:24
Limita funkce
Dobrý den,
prosím o pomoc s výpočtem limity funkce.
lim (sinx + 2x^2 * cos 2x + 3x^2 * ctg3x) /2x
postupovala bych rozkladem zlomku abych mohla části upravit dle vět.
lim sinx + 2x/2x * (cos 2x + 3x^2 * ctg3x)
a dál si nevím rady.
prosím o radu jak postupovat při řešení této limity.
Děkuji
Offline
#6 22. 11. 2009 15:44 — Editoval Nestor10 (22. 11. 2009 15:52)
Re: Limita funkce
↑ Miky:
Rozložil zlomek na součet tří zlomků se stejným jmenovatelem, zkrátil co se dalo a to co napsal je jen přepis tvého původního zadání.
A tedy stačí již jen spočíst jednotlivé tři limity.
první vyjde 1/2
druhá 0
třetí dle LP 1/2
Výsledek je 1.
Offline
#9 30. 11. 2009 22:10
Re: Limita funkce
Dobrý večer,
mám naprosto stejný příklad.
Postupně mi vyšlo:
1/2 * sin x/x + x*cos2x/1 + 3x*cotg3x/2 což by mělo být totéž, co psala Tychi
ale pak dál už to asi počítám špatně (výsledek vím, ale chci pochopit postup).
ta limita se blíží k nule, ale není nula. Takže když si představím x jako například 0,001, jak z toho zjistím sin 0,001?
Vím, že sin x/x musí vyjít 1, ale cesta mi uniká.
Vysvětlíte mi to, prosím?
Děkuji.
Offline
#10 30. 11. 2009 22:14
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita funkce
↑ Maca:
Ona se neblíží k nule. "Blíží" se podílu  , což je nedefinovaný výraz. Když si ale dané funkce nakreslíš, tak zjistíš, že v jistém okolí bodu [0;0] jsou prakticky identické - jejich podíl tedy bude 1.
, což je nedefinovaný výraz. Když si ale dané funkce nakreslíš, tak zjistíš, že v jistém okolí bodu [0;0] jsou prakticky identické - jejich podíl tedy bude 1.
Je to tabulková limita, dá se ověřit třeba L'Hospitalovým pravidlem.
Offline
#11 30. 11. 2009 22:56
Re: Limita funkce
Asi neumím pořádně použít HP.
Celou dobu jsem teď znovu hledala v učebnicích i na internetu. Všechny mě dostupné příklady jsou s mocninami, o tabulkové limitě ani ťuk.
Pořád mi tam "vadí" ten sin.
Šlo by to, prosím, ještě trochu polopatyčtěji vysvětlit. Děkuji
Offline
#13 30. 11. 2009 23:07
Re: Limita funkce
Ještě jsem ho nepoužila, ale jak tomu rozumím: omlouvám se za ne moc matematickou terminologii
dosazením do zlomku limity mi musí vyjít 0/0 nebo oo/oo
pak mocninu dám před neznámou a původní mocninu o 1 snížím (obojí se týká čitatele i jmenovatele)
to bych opakovala do "vymizení "mocnin a dále počítala jen s koeficienty neznámých.
Je to správně?
Offline
#14 30. 11. 2009 23:14
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Limita funkce
↑ Tychi:Jen bych doplnil, že počítáme  , což je jen dvojí využití tabulkové limity
, což je jen dvojí využití tabulkové limity  .
.
Jakkoliv nemám rád vzorečky, používat tuto limitu bez odvozování stále dokola mi připadá rozumné.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#16 01. 12. 2009 00:33
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Limita funkce
↑ Maca:"mocninu dám před jmenovatele ..." -- to funguje jen u mocninných funkcí. Obecně jmenovatele i čitatele derivuješ. Opravdu derivace 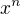 je
je  , ale derivace
, ale derivace 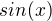 je
je  . Proto
. Proto  .
.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#24 03. 12. 2009 12:28
Re: Limita funkce
Dobrý den
můžete mi, prosím zkontrolovat postup? x jde k "0"
1 sin x 2x^2 * cos 2x 3x^2 * ctg 3x 1 cos x 2x^2 * 2(-sin x) 3x^2 * (-1/sin^2x)
lim -- * ------ + ---------------- + -------------- = lim -- * ------- + ----------------- + ---------------------- =
2 x 2x 2x 2 1x^0 2x 2x
1 1 2 (2x^1)*0 1 6x^1 * (-1/0)
=( --- * ------- ) + ( ---- * ------------ ) + ( ------ * ----------------------) = 1/2 + (1 * 0/1) + (1/2 * ?/1 )
2 1 2 1x^0 2 1x^0
Mě tam ta 1/1 nevychází...... Poradíte mi, prosím, kde dělám chybu?
Děkuji.
Offline
#25 03. 12. 2009 12:52
Re: Limita funkce
↑ Maca:To počítáš L'Hospitalem? Pokud ano, tak musíš pořád derivovat vršky i spodky celé. Derivace součinu totiž vypadá jinak než jako součin derivací.
Ve druhém a třetím zlomku je dle mého lepší rovnou pokrátit to x a pak ty limity spočítat jednodušeji.
Vesmír má čas.
Offline






 - je to tabulkova limita, alebo sa to da vypocitat l'Hospitalom
- je to tabulkova limita, alebo sa to da vypocitat l'Hospitalom