Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » urcenie parnosti cisla v grupe (TOTO TÉMA JE VYŘEŠENÉ)
#1 26. 11. 2009 13:55
- scortyak47
- Zelenáč
- Příspěvky: 8
- Reputace: 0
urcenie parnosti cisla v grupe
Zdravim vedel by mi niekto poradit ako urcim ci je x parne (sude) alebo nie z tohoto
g^(x*(p-1)/2) mod p
kde g je generatorom multiplikativnej grupy Zp*, p je prvocislo
vopred dakujem za odpoved.
Offline
#2 26. 11. 2009 17:56
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: urcenie parnosti cisla v grupe
Po umocnění na druhou to musí dát 1 (Malá Fermatova věta, resp. Lagrangeova http://en.wikipedia.org/wiki/Lagrange%2 … _theory%29).
Protože to samo o sobě nemůže být 1 (jinak by g nebyl generátor), musí to být -1.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#3 26. 11. 2009 18:58 — Editoval scortyak47 (26. 11. 2009 19:00)
- scortyak47
- Zelenáč
- Příspěvky: 8
- Reputace: 0
Re: urcenie parnosti cisla v grupe
ako viem ze g^(p-1) (mod p) je jedna ale ako mi to pomoze pri urceni parnosti alebo neparnosti toho x?
Offline
#4 26. 11. 2009 20:53 — Editoval Kondr (26. 11. 2009 22:28)
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: urcenie parnosti cisla v grupe
↑ scortyak47: to je přímo malá Fermatova věta (speciální případ Lagrangeovy).
to je přímo malá Fermatova věta (speciální případ Lagrangeovy).
Pak  . Kdyby bylo
. Kdyby bylo  , nebyl by g generátor. Proto
, nebyl by g generátor. Proto 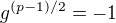 , takže
, takže  .
.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 26. 11. 2009 21:54
- scortyak47
- Zelenáč
- Příspěvky: 8
- Reputace: 0
Re: urcenie parnosti cisla v grupe
cize dalo by sa povedat ze ak x bude parne potom hodnota vyrazu zo zadania bude parna?(a opacne)
Offline
#6 26. 11. 2009 22:27
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: urcenie parnosti cisla v grupe
↑ scortyak47:Pokud bude x sudé, bude ta hodnota 1. Jinak bude -1.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#7 26. 11. 2009 22:45
- scortyak47
- Zelenáč
- Příspěvky: 8
- Reputace: 0
Re: urcenie parnosti cisla v grupe
aha,jasne
naozaj velke diky :)
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z algebry
- » urcenie parnosti cisla v grupe (TOTO TÉMA JE VYŘEŠENÉ)