Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Erdős–Szekeres theorem (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 01. 2010 22:56
Erdős–Szekeres theorem
Ahoj,
nevíte někdo náhodou o nějakém srozumitelném důkazu Erdős–Szekeresova lemmatu? (zkráceně – Každá posloupnost reálných čísel urč. délky má podposloupnost urč. délky monotónní.) Dívám se na anglickou Wiki a nějak to nemůžu pochopit...
Díky.
V.
Offline
#3 02. 01. 2010 12:19
Re: Erdős–Szekeres theorem
Je mi celkem jasná první část důkazu přes holubník, ale z textu příliš nechápu, proč by dvě čísla z řady nemohly mít stejnou dvojici (ai, bi).
Offline
#5 02. 01. 2010 15:05
Re: Erdős–Szekeres theorem
Aha, už jsem to pobral. Díky.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Erdős–Szekeres theorem (TOTO TÉMA JE VYŘEŠENÉ)

 a
a 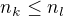 , tak tu nejdelší rostoucí posloupnost končící
, tak tu nejdelší rostoucí posloupnost končící  můžeš prodloužit o
můžeš prodloužit o 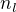 , takže
, takže  , obdobně pro
, obdobně pro 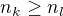 bude
bude  . a jedna z těchhle možností určitě nastane
. a jedna z těchhle možností určitě nastane