Matematické Fórum

Lancer · 11. 01. 2010 19:42 — Editoval Lancer (11. 01. 2010 19:42)

Dokážte, že ak x, y, z sú také kladné čísla, že $xyz=1$ , tak platí $x+y+z+xy+yz+xz \ge 6$

Najde sa niekto kto by mi dal nejaky hint? Diky moc.

Kondr · 11. 01. 2010 22:24

Odkud je ta úloha? Hintů připojím celé PDFko, to by nemělo vadit, ani když by byla soutěžní: http://bart.math.muni.cz/~brkos/files/p … ani163.pdf

Lancer · 12. 01. 2010 16:56 — Editoval Lancer (12. 01. 2010 16:57)

↑ Kondr:
Nejako som to zosmolil bez tych hintov co ste mi dali, mozete mi to prosim vas okontrolovat? Alebo aj niekto iny.

Podla $xyz=1$ plati:
xy=1/z
yz=1/x
xz=1/y

Dosadim: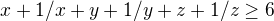
$x+1/x+y+1/y+z+1/z \ge 6$

Teba dokazat, ze:
x+1/x>=2

Dokaz:
(x-1)^2>=0
x^2-2x+1>=0
x-2+1/x>=0
x+1/x>=2

q.e.d.

Edit: Ulohu mam zo skoly.

Wotton · 12. 01. 2010 16:59

↑ Lancer:

Tos přesně dokázal ty hinty co ti radil ↑ Kondr:, takže k tomu není co dodat.

Pavel · 13. 01. 2010 09:53

↑ Lancer:

Stačí taky využít A-G nerovnost pro levou stranu dokazované nerovnosti. Platí tedy, že

$\frac{x+y+z+xy+yz+xz}6 \geq\sqrt[6]{x\cdot y\cdot z\cdot xy\cdot yz\cdot xz}=\sqrt[6]{x^3y^3z^3}=1$ . Odtud dokazovaná nerovnost plyne okamžitě.

Matematické Fórum

#1 11. 01. 2010 19:42 — Editoval Lancer (11. 01. 2010 19:42)

Dokazte, ze...

#2 11. 01. 2010 22:24

Re: Dokazte, ze...

#3 12. 01. 2010 16:56 — Editoval Lancer (12. 01. 2010 16:57)

Re: Dokazte, ze...

#4 12. 01. 2010 16:59

Re: Dokazte, ze...

#5 13. 01. 2010 09:53

Re: Dokazte, ze...

Zápatí