Matematické Fórum

Lishaak · 23. 01. 2008 17:36

Proletel jsem Lukeeho clanek o definicnih oborech a zatim jsem si vsiml tohoto:

Je tam spatne definicni obor funkce tanges, ktery ma byt spravne 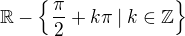$\mathbb{R} - \{\frac{\pi}{2} + k\pi\: |\: k \in \mathbb{Z}\}$

Nestalo by za to tam napsat definicni obory vice elementarnich funkci?

Ivana · 23. 01. 2008 18:07

↑ Lishaak:Já bych to tak nedělala, to už by bylo jako učebnice, dala bych definiční obor
vždy k danému počítanému příkladu.Ale je to jen názor. :-)

Lukee · 23. 01. 2008 18:23

↑ Lishaak: Díky, opraveno. Nevím jak se mi to povedlo, ještě jsem si schválně pro jistotu nechal vypsat graf. Doplnil jsem tam ještě pár dalších funkcí, další mě nenapadají.

Pavel Brožek · 23. 09. 2008 23:58

↑ Lukee:

Dnes se tu řešily definiční obory, tak jsem si prošel tvůj článek a narazil jsem na toto:

"Zlomek má definiční obor R − {0}; reálná čísla bez nuly." (to asi není vhodná formulace)

a o kousek dál

"Logaritmus musí být nezáporný" (nezáporný musí být argument logaritmu)

Matematické Fórum

#1 23. 01. 2008 17:36

Pripominky k clanku o definicnich oborech

#2 23. 01. 2008 18:07

Re: Pripominky k clanku o definicnich oborech

#3 23. 01. 2008 18:23

Re: Pripominky k clanku o definicnich oborech

#4 23. 09. 2008 23:58

Re: Pripominky k clanku o definicnich oborech

Zápatí