Matematické Fórum

karlherbert · 18. 01. 2010 18:49

dobry den mohl by mi pomoc nekdo s tim prikladem nevim zda postupuju dobre.... určete hodnotu pro f'(pí/4) z funkce f(x)=odmocnina ze sin x
takze sem to zderivoval na tvar 1/2 sin na minus 1/2 * cosx ... po dosazeni 1/ 2* odmocnina sin pí/4 * cos pí/3 = 1/2*odmocina pí/4 * odmocnina 2/2

a dal nevim tak dik za nápovedu

jelena · 18. 01. 2010 19:36

↑ karlherbert:

Zdravím, zkus začít psat v místním TeX (když klepneš na můj zápis, tak se přenese do zprávy a můžeš pokračovat v zápisu - pokud budeš potřebovat pomoc s TeX, tak tady se dostane.
K zadání (souhlasí můj přepis?):

$f(x)=\sqrt{\sin x}$

$f^{\prime}(x)=\frac{\cos x}{2\sqrt{\sin x}$

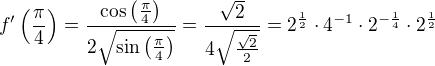$f^{\prime}$\frac{\pi}{4}$=\frac{\cos $\frac{\pi}{4}$}{2\sqrt{\sin $\frac{\pi}{4}$}}=\frac{\sqrt{2}}{4\sqrt{\frac{\sqrt{2}}{2}}}=2^{\frac12}\cdot4^{-1}\cdot2^{-\frac14}\cdot2^{\frac12}$ přepsala jsem na součín mocnin 2, to už by mělo být řešitelné. Může být?

karlherbert · 18. 01. 2010 20:15

Jasně děkuju ti nebyl jsem si jist sto procentne jak se zabavit toho sina tak dekuju...

Matematické Fórum

#1 18. 01. 2010 18:49

dosazeni

#2 18. 01. 2010 19:36

Re: dosazeni

#3 18. 01. 2010 20:15

Re: dosazeni

Zápatí