Matematické Fórum

check_drummer

Ahoj,
mějme zadánu rekurentní rovnici následujícím způsobem: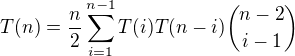

$T(n)=\frac{n}{2}\sum_{i=1}^{n-1}{T(i)T(n-i){{n-2}\choose{i-1}}}$

$T(1)=1$

$(T(2)=1, T(3)=3, atd. ...)$

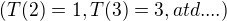
Určete explicitní vzorec pro T(n) jakožto funkci proměnné n.

Autor skryl část textu. Zobrazit/skrýt!

Kondr · 18. 01. 2010 23:51

Při psaní tohoto vycházím z http://www.dmg.tuwien.ac.at/drmota/berlin08.pdf
Položme 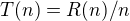$T(n)=R(n)/n$ a dodefinujme $R(0)=0$
$(n-1)\frac{R(n)}{n!}=\frac{n}{2}\sum_{i=1}^{n-1}\frac{R(i)}{i!}\frac{R(n-i)}{(n-i)!}$
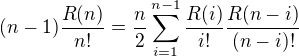
Uvážíme exponenciální vytvořující funkci pro R(n), z výše uvedeného vztahu sestavíme funkcionální rovnici a máme jakýsi výsledek. Jak dál k explicitnímu tvaru nevím.

Matematické Fórum

#1 18. 01. 2010 21:11 — Editoval check_drummer (18. 01. 2010 21:18)

Rekurentní rovnice

#2 18. 01. 2010 23:51

Re: Rekurentní rovnice

Zápatí