Matematické Fórum

Olin · 25. 01. 2010 09:24

Zdravím kolegy,

připravuji se na zkoušku z Úvodu do matematické logiky a projíždím si typy otázek do písemky. Skoro všechno je OK, až na následující:

# Najit sentenci (v nejakem jazyce), ktera ma jen konecne modely ci naopak jen nekonecne modely.

Sentence jen s konečnými modely by mohla být tato: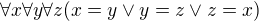
$\forall x \forall y \forall z (x = y \vee y = z \vee z = x)$ .
Horší je to pouze s nekonečným modelem. Tam kolegu napadlo něco jako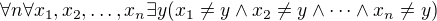
$\forall n \forall x_1, x_2, \dots, x_n \exists y (x_1 \neq y \wedge x_2 \neq y \wedge \dots \wedge x_n \neq y)$ ,
ale to mi připadá, že není jedna sentence, ale spousta sentencí v jedné.

Pak tady ještě je:

# Priklad na pouziti vety o kompatnosti logiky 1.radu. Napr.: najit sentenci, ktera ma libovolne velky konecny model ac nema nekonecny model, nebo jeji existenci vyvratit.

Tady mi přijde, že taková sentence neexistuje, ovšem asi nedokážu to nedokážu přesně zdůvodnit pomocí věty o kompaktnosti ("teorie má model právě tehdy, když každá konečná podteorie má model"). Moje idea, proč neexistuje, je taková, že podobně jako při důkazu věty o kompaktnosti vezmu všechny funkce z přirozených čísel do nosičů všech možných konečných modelů a ty následně rozstrkám do tříd ekvivalence pomocí ultrafiltru. Těchto ekvivalencí je nekonečně mnoho a dá se to domyslet do nekonečného modelu. Ovšem předpokládám, že existuje nějaký snadný argument plynoucí z věty o kompaktnosti…

Budu vděčný za jakékoliv nápady a připomínky!

Wotton · 25. 01. 2010 12:20

Teorie s konečným modelem je správně.

Ta druhá se ti oprávněně nelíbí. Ale může být například takhle: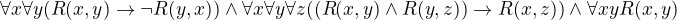
$\forall x\forall y(R(x,y)\rightarrow\neg R(y,x))\wedge\forall x\forall y\forall z((R(x,y)\wedge R(y,z))\rightarrow R(x,z))\wedge\forall x\exist y R(x,y)$
Pak je ta relace R vlastně uspořádání které nemá největší prvek.

No a k tomu poslednímu, taková sentence opravdu neexistuje. Dokonce si vzpomínám, že existuje věta:

Pokud má teorie libovoně velký konečný model, tak má i nekonečný model.

Ale ted si nevspominám na důkaz. Ještě o tom popřemýšlím.

Wotton · 25. 01. 2010 13:00 — Editoval Wotton (25. 01. 2010 13:02)

Tak už to mám:

Nechť sentence $\varphi$ je taková, že má pouze konečné modely, ale libovolné velikosti.

K tomu si vezmem takovouhle teorii s nekonečně axiomy: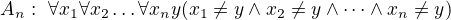

$A_n:\ \forall x_1\forall x_2\dots\forall x_n\exist y(x_1\neq y\wedge x_2\neq y\wedge\dots\wedge x_n\neq y)$

Nyní když vezmem teorii která je sjednocením těcho axiomů se sentencí $\varphi$ , tak každá její konečná část má model. Podle věty o kompaktnosti musí tedy mít i tato teorie model. To je ale spor, protože by musel být současně konečný i nekonečný, tudíž sentence $\varphi$ s požadovanými vlastnostmi neexistuje.

Olin · 25. 01. 2010 13:13

Díky! Tak já vyrážím na zkoušku!

Matematické Fórum

#1 25. 01. 2010 09:24

Pár otázek k logice

#2 25. 01. 2010 12:20

Re: Pár otázek k logice

#3 25. 01. 2010 13:00 — Editoval Wotton (25. 01. 2010 13:02)

Re: Pár otázek k logice

#4 25. 01. 2010 13:13

Re: Pár otázek k logice

Zápatí