Matematické Fórum

Ferdish · 28. 01. 2010 11:50

Zdar!

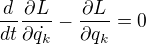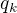Mám problém s touto tematikou. Klasická Lagrangeova rovnica 2.druhu, teda $\frac{d}{dt}\frac{\partial{L}}{\partial{\dot{q_k}}}-\frac{\partial{L}}{\partial{q_k}}=0$ , kde $L$ je Lagrangeova funkcia, $q_k$ k-ta zovšeobecnená súradnica a 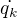$\dot{q_k}$ jej rýchlosť. Počet súradníc je rovný počtu stupňov voľnosti n, teda $k=1,2,3,...,n$ .
V poznámkach mám poznačené, že sústava s n stupňami voľnosti má 2n prvých pohybových integrálov ako funkcii času, všeob. súradníc a rýchostí, no v prednáškach už nemám napísané, prečo. Prednášky mám okopírované, lebo som v ten deň nebol na prednáške, a v literatúre čo mám som nič nenašiel.
Bol by tu niekto kto by mi to vysvetlil? Profák na tejto otázke pred mojimi očami nachytal a následne vyrazil zo skúšky jednu kolegyňu a nechcem, aby sa to isté stalo aj mne.

rughar · 28. 01. 2010 15:58 — Editoval rughar (28. 01. 2010 16:04)

Ahoj.

Jestli na tomto nějaký profesor někoho nachytá, vyrazí a na místě nevysvětlí jak to mělo být, tak bych takového profesora opravdu nechtěl.

Jde o to, že počet stupňů volnosti je něco jako nutný počet parametrů k vyjádření vzhledu systému v konfiguračním prostoru. Pokud máš jednu částici volně ve vesmíru, pak konfigurační prostor je celý vesmír a parametry popisující "vzhled" toho bodu (nevím jak to napsat lépe), což pro jeden bod znamená jeho polohu ve vesmíru, jsou tři (poloha x,y,z). Máš-li závaží na kyvadle, pak konfigurační prostor tohoto kyvadla je kružnice (to je konf. prostor) a parametr popisující jeho polohu je jeden. Možno volit třeba úhel, který závaží s vláknem svírá s vertikálním směrem. Obecně platí že počet stupňů volnosti v trojrozměrném případě je 3N - k, kde k je počet vazeb systému, N je počet částic v systému. Když například vezmeme pohyb planetky kolem těžké hvězdy (jeden objekt), tak Začínáme ne třech stupních volnosti. Platí ale, že pohyb je roviný (dejme tomu v rovině x,y), takže složka polohy z je nulová. To je jedna vazba. Druhá vazba je zákon zachování momentu hybnosti (nebo též 2. Keplerův zákon). Tím máme dvě vazby. A zůstává nám jeden stupeň volnosti. Ten vyjadřuje, že planeta se bude pohybovat po nějaké křivce parametrizované jedním parametrem a my potřebujeme nejaký jeden integrál pohybu.

To byly stupně volnosti systému. Trochu odlišným pojmem je počet fyzikálních stavů systému. Přesná poloha totiž nevyjadřuje úplný fyzikální stav hmotného bodu. Je potřeba znát ještě hybnost každého bodu. Tedy ke každé zobecněné souřadnici (měnící se poloze) potřebujeme znát k ní příslušnou hybnost. Pokud jsme tedy dospěli k závěru, že máme pro systém n stupňů volnosti (n = 3N - k ), pak počet fyzikálních stavů systému je 2n. Možná je tohle odpovědí na tvoji otázku.

V každém případě když je n stupňů volnosti, tak není pravda, že bys potřeboval dvakrát tolik integrálů pohybu. Je to jako s tím kyvadlem. Stačí ti právě jeden integrál pohybu. Je to dost zřejmé. Když máš systém závislý jen na jedné souřadnici, tak potřebuješ právě jednu rovnici která ti poví, jak se tato souřadnice bude vyvíjet s časem. Otázka je, jestli tou druhou rovnicí náhodou nemyslí něco jako počáteční podmínky. Tj. hodnotu souřadnice v konkrétním čase (třeba t = 0)

Matematické Fórum

#1 28. 01. 2010 11:50

Počet prvých pohybových integrálov Lagrangeovej rovnice 2.dr.

#2 28. 01. 2010 15:58 — Editoval rughar (28. 01. 2010 16:04)

Re: Počet prvých pohybových integrálov Lagrangeovej rovnice 2.dr.

Zápatí