Matematické Fórum

Ferdish · 04. 02. 2010 14:58

Môžte mi poradiť, akú úpravu použiť alebo o aký fakt sa mám oprieť pri riešení limity $\lim_{n\rightarrow\infty}\frac{|x|^{n+1}exp^{|x|}}{(n+1)!}$ , ak má byť rovná nule pre $|x|>1$ ?

Pavel · 04. 02. 2010 15:32 — Editoval Pavel (04. 02. 2010 15:33)

↑ Ferdish:

co tak použít Stirlingův vzorec:

$\lim_{n \to \infty} \frac{n!}{\sqrt{2\pi n} \left( \frac{n}{e} \right)^n} = 1$

a eliminovat tak faktoriál.

halogan · 04. 02. 2010 15:36

e^|x| je konstanta, ta může jít před limitu a dále můžeme použít ostrou (resp. <<) nerovnost a^n << n!. Pokud to tak můžete používat.

Ferdish · 04. 02. 2010 16:42

Stirlingov vzorec - vidím a počujem prvýkrát v živote.
A čo sa týka tej nerovnosti, to ma napadlo, no neviem čo v prípade ak mi to bez nejakého dôkazu neuzná. Je to totiž jeden z 50 príkladov (resp. jeho časť), ktorý mám odovzdať pred skúškou na termíne. Neviem či to číta, ak nie tak je to ok, ale ak hej tak neviem čo jej poviem, ak sa ma spýta na dôkaz. Skúsim a uvidím.

lukaszh · 04. 02. 2010 16:50

↑ Ferdish:
Pre zistenie limity
$\lim_{n\to\infty}\frac{\alpha^n}{n!}=0$
dokážeme odhad
$\frac{\alpha^n}{n!}\,<\,\frac{\alpha}{n}$

Rumburak · 04. 02. 2010 17:02

↑ Ferdish:
Dá se použít i teorie řad.
Označíme 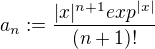$a_n :=\frac{|x|^{n+1}exp^{|x|}}{(n+1)!}$ a dle d'Alemgertova kriteria ukážeme, že řada $\sum a_n$ konverguje.
Odtud nutně $\lim_{n\rightarrow\infty}a_n = 0$ .

Olin · 04. 02. 2010 17:03

Odhadneme
$\frac{x^n}{n!} \leq \frac{x^n}{[x]! ([x]+1)^{n-[x]}} = \frac{([x]+1)^{[x]}}{[x]!} $ \frac{x}{[x]+1} $^n$
což jde zřejmě k nule. [x] značí celou část x. Absolutní hodnoty se mi nechtělo psát.

Matematické Fórum

#1 04. 02. 2010 14:58

Limita funkcie

#2 04. 02. 2010 15:32 — Editoval Pavel (04. 02. 2010 15:33)

Re: Limita funkcie

#3 04. 02. 2010 15:36

Re: Limita funkcie

#4 04. 02. 2010 16:42

Re: Limita funkcie

#5 04. 02. 2010 16:50

Re: Limita funkcie

#6 04. 02. 2010 17:02

Re: Limita funkcie

#7 04. 02. 2010 17:03

Re: Limita funkcie

Zápatí