Matematické Fórum

Olin · 09. 02. 2010 11:38 — Editoval Olin (09. 02. 2010 21:49)

Nechť je v obvyklé rovině 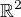$\mathbb{R}^2$ rozmístěno libovolné množství následujících libovolně velkých hvězd:

("hvězda" jsou tři různé stejně dlouhé úsečky s jedním společným koncovým bodem, které po dvou svírají úhel 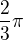$\frac 23 \pi$ ). Nejsou ovšem vůči sobě libovolně natočeny, každé dvě hvězdy mají rovnoběžné a stejně orientované "cípy" (tj. existuje stejnolehlost s kladným koeficientem, která zobrazí jednu na druhou). Navíc se žádné dvě hvězdy neprotínají (jsou disjunktní).

Dokažte, že za těchto podmínek může být v rovině rozmístěno nanejvýš spočetně mnoho těchto hvězd.

Kondr · 10. 02. 2010 22:09

Pěkné :) Moc nevím, k čemu je to stejné natočení...

Autor skryl část textu. Zobrazit/skrýt!

Olin · 10. 02. 2010 22:25

↑ Kondr:
Já to vlastně taky nevím, ale zprostředkovaně se ke mně úloha dostala s tímto zadáním. Třeba aspoň pro zmatení nepřítele. Jinak úlohu jsem po několika měsících přemýšlení vyřešil podobnou úvahou.

petrkovar · 10. 02. 2010 22:57

↑ Kondr:V zadání není řečeno, že cípy jsou stejně dlouhé. Kolem každé hvězdy bych mohl umístit tři menší, řekněme o délce cípu 1/10 předchozí. Najednou se mi jich v duhé úrovni vyrojí devět, ve třetí 27. Vždy budu umět přidat další hvězdy přidat.
Bude uvedený argument fungovat?

Olin · 10. 02. 2010 23:05 — Editoval Olin (10. 02. 2010 23:16)

↑ petrkovar:
Je to tam řečeno,

Olin napsal(a):
"hvězda" jsou tři různé stejně dlouhé úsečky s jedním společným koncovým bodem

Mimochodem, asi by to fungovalo i s těmi různými délkami, prostě bychom

Autor skryl část textu. Zobrazit/skrýt!

Kondr · 11. 02. 2010 00:02

A potřebujeme vůbec, aby každý úhel byl 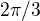$2\pi/3$ (bude-li nenulový? Nestačilo by, aby každé dvě hvězdy byly stejné až na otočení, posunutí a zkrácení ramen?

petrkovar

↑ Olin:Já jsem to pochopil tak, že každá hvězda má tři ramena stejné délky, ale každé dvě hvězdy mohou mít tuto délku různou. To mi pak poznámka o stejnolehlosti přijde spíš zavádějící.

Kondr · 11. 02. 2010 16:49

↑ petrkovar: Takto jsem to pochopil i já a k takovémuto zadání se vztahuje mé řešení. Kdybychom měli všechny hvězdy stejně velké, nebylo by třeba je dělit do tříd podle magnitudy.

petrkovar · 11. 02. 2010 20:45

↑ Kondr:A když ke každé hvězdě s délkou cipu c budou existovat tři menší o délce cípu c/10 (podobně jako u fraktálů přidáváme části), tak magnituda neexistuje.

Kondr · 11. 02. 2010 21:12

↑ petrkovar: Nevím, jestli jsem si nějak nenaběhl se slovem magnituda, ale tak jak jsem ho zamýšlel (převrácená hodnota délky cípu zaokrouhlená nahoru) musí mít každá hvězda magnitudu. Pak jen tvrdím, že hvězd pevně zvolené magnitudy je jen spočetně (a to stačí, protože různých magnitud je spočetně).

Olin · 11. 02. 2010 21:31

Zadání jste pochopili oba správně. Samozřejmě mohou mít různé hvězdy různé velikosti, na to se nekladou žádná omezení. Pokud by byly všechny stejně velké, byla by úloha o dost snazší.

Vnitřní úhly asi taky nemusí být nutně ty zadané. Zajímavější už je ovšem, když připustíme, aby se hvězdy mohly lišit i v těchto úhlech…

petrkovar

↑ Olin:Myslím, že toto říká, že ani různé úhly nezabrání v konečném důsledku tomu, aby hvězd bylo jen spočetně mnoho. Taky bych řekl, že požadavek na stejné úhly a stejné "otočení" umožní použít nějaké "pěkné pozorování", které povede snadno k požadovanému výsledku.

Matematické Fórum

#1 09. 02. 2010 11:38 — Editoval Olin (09. 02. 2010 21:49)

Hvězdy v rovině

#2 10. 02. 2010 22:09

Re: Hvězdy v rovině

#3 10. 02. 2010 22:25

Re: Hvězdy v rovině

#4 10. 02. 2010 22:57

Re: Hvězdy v rovině

#5 10. 02. 2010 23:05 — Editoval Olin (10. 02. 2010 23:16)

Re: Hvězdy v rovině

Olin napsal(a):

#6 11. 02. 2010 00:02

Re: Hvězdy v rovině

#7 11. 02. 2010 16:04 — Editoval petrkovar (11. 02. 2010 16:07)

Re: Hvězdy v rovině

#8 11. 02. 2010 16:49

Re: Hvězdy v rovině

#9 11. 02. 2010 20:45

Re: Hvězdy v rovině

#10 11. 02. 2010 21:12

Re: Hvězdy v rovině

#11 11. 02. 2010 21:31

Re: Hvězdy v rovině

#12 11. 02. 2010 22:08 — Editoval petrkovar (11. 02. 2010 22:09)

Re: Hvězdy v rovině

Zápatí