Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 10. 02. 2010 13:26
Re: geometriclá posloupnost
↑ leník 5: pro soucet prvnich n clenu geometricke posloupnosti plati  , tedy mame rovnici
, tedy mame rovnici  , pokratime
, pokratime  a vyresime vzniklou rovnici pro kvocient
a vyresime vzniklou rovnici pro kvocient  , posleze uz snadno dopocteme
, posleze uz snadno dopocteme 
Offline
#4 10. 02. 2010 13:32
Re: geometriclá posloupnost
↑ leník 5:
pokud 





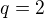 ,
,  je libovolné reálné číslo.
je libovolné reálné číslo.
pokud 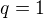

Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 10. 02. 2010 14:28
Re: geometriclá posloupnost
↑ zdenek1: Asi jsem úplně nemožná, ale nevím, jak z toho vypočítat  . Prosím...
. Prosím...
Offline
#6 10. 02. 2010 14:47
Re: geometriclá posloupnost
zdenek1 napsal(a):
...
je libovolné reálné číslo.
Dva jsou tisíckrát jeden.
Offline
 . Určete
. Určete  a
a 