Matematické Fórum

nika.v · 31. 01. 2008 08:14 — Editoval nika.v (31. 01. 2008 15:46)

Ahoj lidi, nemůžu si pomoc, ale asi jsem dutá. Mám příklad i s výpočtem, vůbec netuším, jak došli z předposledního kroku k poslednímu. Pomůžete mi?

Rozhodni, zda množina 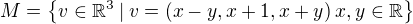$M = \{v \in \mathbb{R}^3\: | \: v = (x-y, x + 1, x+y) \: x, y \in \mathbb{R}\}$ je podprostorem či nikoliv.

Dle učebnice: zvolme a = 2, a*v=2*v=(2x-2y, 2x+2, 2x+2y) sem jsem to vstřebala = (x´- y´, x´+ 2, x´+ y´)
a tady už jsem mimo. Řekla bych, že zvolili za 2x=x´a 2y=y´, nevím proč, ale dejme tomu. Každopádně píší, ze (x´- y´, x´+ 2, x´+ y´) nepatří do množiny M a tudíž M nemůže být podprostorem 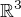$\mathbb{R}^3$ .

Nechápu, proč by to tam nemohlo patřit, když x´- y´náleží R, x´+ 2 náleží R a x´+ y´také náleží R.

Děkuju. pa eja

OK, to jsem jakžtakž vztřebala a co třebas toto: rozhodni, zda následující podmnožina Rna2 jsou podprostory Rna2.
W={v náleží Rna2, v=(x-2y, 2x+y), x,y náleží R}

Zkusím to: vynásobím třeba 2 vektor v, tedy: 2*v = (2x-4y, 4x+2y), zvolím si vektor třeba (-2, 3) a vyjde mi
2x - 4y = -2
4x + 2y = 3 a vyšlo mi x=2/5 a y 7/10
Tyhle čísla logicky šlo najít, vzhledem ke dvou rovnicím o dvou neznámých. Tedy W je podprostorem Rna2.

Tak je to správně? Kuju a pa

thriller · 31. 01. 2008 09:23

Zda je množina vektorů vektorovým prostorem (nebo podmnožina vektorovým podprostorem) rozhodneš podle definice vektorového prostoru, tj. mimo jiné 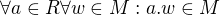$\forall a \in R \forall w \in M : a.w \in M$ .
Jelikož se snažíme dokázat neplatnost tohoto tvrzení, stačí najít jedno číslo a pro které to neplatí.
Takže, když vezmeš a=2 a vynásobíš jim vektor w, musíš rozhodnout, zda tento násobek patří do M. Tzn. hledáš dvě reálná čísla x' a y', pomocí nichž přepíšeš (2x-2y,2x+2,2x+2y) do tvaru (x'-y',x'+1,x'+y'), která nejde najít.
Například, když vektor z M bude (-1,2,3) (za x a y sem zvolil 1 a 2) a vynásobíš ho dvěmi, budeš mít (-2,4,6) a teď jestli tento vektor je z M musí se dát najít dvě čísla x a y tak, že bude platit $x-y=-2, x+1=4 a x+y=6. => x=3, y=5\neq3$ ! Taková čísla nešlo najít, proto násobek vektoru z M není z M.

Lishaak · 31. 01. 2008 09:26

Aaa, thriller me predbehl....

Vis jak se pozna, ze nejaka podmnozina R^3 neni podrostorem? Kdyz se z ni da vyskocit bud nasobenim realnym cislem nebo scitanim vektoru. Autor ukazal, ze nasobenim dvojkou se z te mnoziny da vyskoci. Vsechny vektory totiz maji tvar

(x - y, x + 1, x+y)

Kdyz tento vektor vynasobime dvojku, dostneme

(x' - y', x' + 2, x' + y').

Tento vektor ale nepatri do M, protoze ve druhe souradnici se pricita dvojka a nikoliv jednicka.

Matematické Fórum

#1 31. 01. 2008 08:14 — Editoval nika.v (31. 01. 2008 15:46)

Určení podprostor - dotaz k vypočtenému příkladu

#2 31. 01. 2008 09:23

Re: Určení podprostor - dotaz k vypočtenému příkladu

#3 31. 01. 2008 09:26

Re: Určení podprostor - dotaz k vypočtenému příkladu

Zápatí