Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 02. 2010 01:04
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Druhá únorová sumace
Nechť 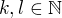 ,
, 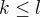 . Najděte, čemu se rovná
. Najděte, čemu se rovná
a dokažte.
Offline
- (téma jako vyřešené označil(a) BrozekP)
#2 11. 02. 2010 02:23 — Editoval Kondr (11. 02. 2010 02:24)
#3 11. 02. 2010 10:25
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Druhá únorová sumace
To není úplně dobře :-)
Offline
#4 11. 02. 2010 20:36 — Editoval check_drummer (11. 02. 2010 20:37)
- check_drummer

- Příspěvky: 4952
- Reputace: 106
Re: Druhá únorová sumace
"Máte úhel beta." "No to nemám."
Offline
#5 11. 02. 2010 21:23
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Druhá únorová sumace
Offline
#6 11. 02. 2010 21:32
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Druhá únorová sumace
↑ BrozekP: Přesně tak, zbytečná chyba.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
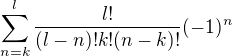
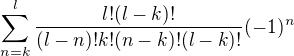
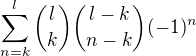
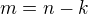
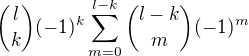
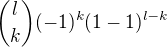


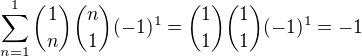
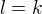 nemůžeme použít binomickou větu.
nemůžeme použít binomickou větu.