Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 17. 02. 2010 17:54 — Editoval Wotton (23. 02. 2010 21:15)
Re: Komplexní čísla - graf
Zdravím. Graficky je to jednoduché, nakreslíš si roviku komplexních čísel, tam bod 3-2i, a dvě kružnice se stredem v tomhle bodě. Jednu s poloměrem 1 a druhou s poloměrem 4. Hledané řešení je pak prostor mezi nimi.
To proto, že dané nerovnice ti říkají, že vzdálenost z od bodu 3-2i je větší než 1, respektivě menší než 4.
No a početně je to vlastně podobný.
Zavspomínáš si jak je vzorec pro absolutní hodotu z komplexního čísla (vpodstatě se jedná o vzdálenost od 0), a spočteš.
EDIT: oprava dle ↑ BrozekP:. Děkuji.
Dva jsou tisíckrát jeden.
Offline
#3 17. 02. 2010 17:57
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Komplexní čísla - graf
↑ Wotton:
Máš určitě na mysli bod 3-2i.
Offline
#5 17. 02. 2010 18:48 — Editoval zdenek1 (17. 02. 2010 18:50)
Re: Komplexní čísla - graf
↑ radeek:
Představ si komplexní číslo ve tvaru 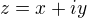

 a po umocnění
a po umocnění
A protože tvůj předcházející příspěvek byl z analytické geometrie, tak toto bys měl poznat.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
