Matematické Fórum

leník 5 · 27. 02. 2010 16:45

Prosím vás o pomoc: Zjistěte souřadnice středu S elipsy a velikosti poloos a, b a výstřednost elipsy e: $x^2+4y^2-6x+4y=0$

Vypočítala jsem: $\frac{(x-3)^2}{9}+\frac{4(y+1)^2}{9}=1$ , dál nevím, prosím...

Olin · 27. 02. 2010 17:05

Není to správně, správně je

$\frac{(x-3)^2}{10} + \frac{4$y + \frac 12$^2}{10} = 1$ .

Marian · 27. 02. 2010 17:07

↑ leník 5:

Počítáš asi špatně, neboť má být

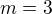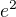Odtud snadno pro střed elipsy $S=[m,n]$ máme $m=3$ , $n=-\frac{1}{2}$ . Taktéž je $a^2=10$ a $b^2=\frac{5}{2}$ . Odtud se snadno vypočte $e^2$ a tudíž také excentricita (výstřednost) elipsy $e$ . Podobným způsobem snadno i $a$ a $b$ .