Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 02. 2010 09:16
analytická geometrie - kružnice
Prosím vás o pomoc: Určete rovnici kružnice, která prochází bodem ![kopírovat do textarea $R[2;1]$](/mathtex/89/89d4c5596106d479e3502a7d42d43709.gif) a dotýká se osy
a dotýká se osy  v bodě
v bodě ![kopírovat do textarea $[1;0]$](/mathtex/86/86be3d40173cac95e0bb383a10713d27.gif)
Budu dosazovat do obecné rovnice  Nevím, jak dál, jestli takto:
Nevím, jak dál, jestli takto: ![kopírovat do textarea $R[2;1]$](/mathtex/89/89d4c5596106d479e3502a7d42d43709.gif)
 to stejné i s druhým bodem, ale nevím co s
to stejné i s druhým bodem, ale nevím co s  . Asi to tak vůbec není, buďte tak hodní, prosím.
. Asi to tak vůbec není, buďte tak hodní, prosím.
Offline
- (téma jako vyřešené označil(a) leník 5)
#2 28. 02. 2010 09:57
Re: analytická geometrie - kružnice
zdravím,
máš zadané dva body, které náleží kružnici. Jenomže dvěma body je zadáno nekonečně mnoho kružnic . proto to musíme nějak "ošmelit" :)
(zaměřil bych se na osu x -> když se jí dotýká, bude to tečna..
-> já osobně raději vycházím z rovnice 
->evidentně jsou zde tři neznámé - m, n, r
-> postupným dosazením za x,y souřadnic bodů, kterými kružnice prochází, získáme soustavu dvou rovnic o dvou neznámých
-> potřebujeme třetí rovnici -> využijeme toho, že je rovnice osy x (tedy  ) -> dosadíš to do rovnice tečny (+za
) -> dosadíš to do rovnice tečny (+za  i
i  ) -> získáš třetí rovnici..
) -> získáš třetí rovnici..
snad :)
Offline
#3 28. 02. 2010 10:47
Re: analytická geometrie - kružnice
Občas pomáhá si situaci nakreslit. Z náčrtu je zřejmé, že x-ová souřadnice středu bude 1 a y-ová souřadnice se bude rovnat poloměru.
Offline
#5 28. 02. 2010 21:59
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: analytická geometrie - kružnice
↑ leník 5:
Zdravím,
z informací od kolegů a ze zadání sestavíme rovnice kružnice, x(středu)=m=1, n nevíme, r nevíme. Budeme dosazovat body, co máme:
bod R:  , po úpravě:
, po úpravě: 
bod na ose x:  , po úpravě:
, po úpravě: 
Řešíme soustavu: (1)
(1) - dosadíme do (1). rovnice
- dosadíme do (1). rovnice
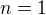
Rovnice kružnice je tedy:  tak jak navrhuješ z nákresu. V pořádku?
tak jak navrhuješ z nákresu. V pořádku?
Offline
#6 28. 02. 2010 23:54
Re: analytická geometrie - kružnice
Šel bych na to (asi jednodušeji -- relativní) takto ...
(1) Potřebujeme k sestavení rovnice souřadnice středy a poloměr kružnice.
(2) Tečnou hledané kružnice v bodě [1,0] je osa "x". Proto střed kružnice S bude ležet na kolmici k tečně procházející bodem [1,0] - to je však přímka p: x=-1.
(3) Kružnice prochází dvěmi různými body, jejichž souřadnice známe - T=[1,0] a R=[2,1]. Najdeme rovnici osy úsečky RT (rovnice se spočítá velmi lehce).
(4) Střed kružnice leží jistě na této ose. Tj., celkem má ležet současně na dvou přímkách. Spočítáme průsečík dvou přímek a máme souřadnici středu S.
(5) Poloměr kružnice "r" je takové číslo, které vyjadřuje vzdálenost libovolného bodu na kružnici od jejího středu S, tj. také od bodu [1,0]. Odtud pomocí Pythagorovy věty obdržíme také velikost poloměru "r".
Offline
#7 01. 03. 2010 00:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: analytická geometrie - kružnice
Marian napsal(a):
Proto střed kružnice S bude ležet na kolmici k tečně procházející bodem [1,0] - to je však přímka p: x=-1
nejsem si úplně jistá, že tomu tak je.
Marian napsal(a):
souřadnice středy
v neděli? nebo také přepínáš na ruskou klavesnici?
Úpřimně - já jsem se v tom postupu ztratila někde v 3. zatáčce, ale tu jsem vyznačila nějaké směry, tak kdyby vyšel čas a byla nálada. Již teď děkuji a hezký radostný pozdrav :-)
Offline
#10 01. 03. 2010 16:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: analytická geometrie - kružnice
↑ leník 5: také děkuji - vždy tak krásně ukončuješ téma - opravdu děkuji moc (věřím, že i za kolegy). Ať se vede :-)
Offline

