Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál s goniometrickými fciami (TOTO TÉMA JE VYŘEŠENÉ)
#2 02. 03. 2010 23:35
- kaja(z_hajovny)

- Místo: Lážov
- Příspěvky: 1002
- Reputace: 12
- Web
Re: Integrál s goniometrickými fciami
tan(x)=t nepomuze?
Offline
#4 03. 03. 2010 08:02 — Editoval Marian (03. 03. 2010 14:10)
Re: Integrál s goniometrickými fciami
↑ Ferdish:
Postupovat lze třeba takto.
(1) Spočteme nejprve primitivní funkci F(x) podle rady ↑ kaja(z_hajovny)::
Dále ve výpočtu primitivní funkce lze postupovat prostřednictvím rozkladu na parciální zlomky. Ovšem pozor na případ a=b, který by se měl ošetřit zvlášť.
(2) Použije se Newton-Leibnizova formule pro výpočet určitého integrálu.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál s goniometrickými fciami (TOTO TÉMA JE VYŘEŠENÉ)

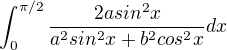
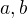 sú kladné reálne parametre.
sú kladné reálne parametre.