Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 03. 2010 12:03
logaritmická funkce
Prosím vás, napsal by mně někdo postup při hledání definičního oboru? 
Když tam není odmocnina, tak vím, že musí být logaritmus > než 0. A zde mně vychází výsledek, když dám > než 1. Ale to asi není správně. Děkuji vám za pomoc.
Offline
- (téma jako vyřešené označil(a) leník 5)
#2 11. 03. 2010 12:06
Re: logaritmická funkce
↑ leník 5:
1. 
2. 
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 11. 03. 2010 13:13
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: logaritmická funkce
↑ leník 5:
Zdravím, chyba u Petákové je vzacnost :-)
asi ještě unikla tato podmínka: 

V pořádku?
Offline
#5 11. 03. 2010 13:15 — Editoval Cheop (11. 03. 2010 13:25)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: logaritmická funkce
↑ leník 5:
Společně s druhou podmínkou  je D(f):
je D(f):
Takže Petáková chybu nemá.
Nikdo není dokonalý
Offline
#7 11. 03. 2010 13:49 — Editoval Cheop (11. 03. 2010 14:18)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: logaritmická funkce
↑ leník 5:
Myslíš kdyby fce byla:
Pak by byla nerovnice:
protože logaritmus 0 není definován
Nikdo není dokonalý
Offline

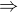
 , ale Petáková tam má tedy chybu
, ale Petáková tam má tedy chybu 
 bez
bez  ? Děkuji vám.
? Děkuji vám.