Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limita z Francie (TOTO TÉMA JE VYŘEŠENÉ)
#1 13. 03. 2010 20:49 — Editoval Marian (13. 03. 2010 20:59)
Limita z Francie
Našel jsem (a vyřešil) jednu limitu z nějakého testu konaného ve Francii. Otestujte se ...
Vypočtěte limitu![kopírovat do textarea $ \reverse\Large\lim_{p\to\infty}\left (\lim_{n\to\infty}\sum_{k=1}^{n}\left (\sqrt{1+\frac{k}{n^2}}+\sqrt[3]{1+\frac{k^2}{n^3}}+\cdots +\sqrt[p]{1+\frac{k^{p-1}}{n^p}}+\sqrt[p+1]{1+\frac{k^p}{n^{p+1}}}-p\right )\right ), $](/mathtex/53/5336d51ce4cbfd68a3a4e8d5446f341e.gif)
kde všechny vystupující proměnné jsou kladná celá čísla.
Offline
- (téma jako vyřešené označil(a) Marian)
#4 17. 03. 2010 10:40
Re: Limita z Francie
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#5 17. 03. 2010 14:12
Re: Limita z Francie
↑ Pavel:
Ano, to je správný krok, především ono rozdělení na dvě limity (u kterých mlčky předpokládáme, že existují, což se, doufám, brzy dovíme).
Nápad k dalšímu kroku bude snad jen to, že žáci středních škol používají binomickou větu. Studenti VŠ však jsou schopni použít prostředek obecnější a umějí tak odhadnout řád (chcete-li, povahu) iracionálních výrazů. Dále už je řešení více zajímavé a přenechávám ostatním k doplnění.
Offline
#6 17. 03. 2010 14:49 — Editoval Pavel (18. 03. 2010 18:04)
Re: Limita z Francie
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Limita z Francie (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $\Large \lim_{n\to\infty}\sum_{k=1}^{n}\left (\sqrt{1+\frac{k}{n^2}}+\sqrt[3]{1+\frac{k^2}{n^3}}-2\right )=\lim_{n\to\infty}\sum_{k=1}^{n}\left (\sqrt{1+\frac{k}{n^2}}-1\right )+\lim_{n\to\infty}\sum_{k=1}^{n}\left (\sqrt[3]{1+\frac{k^2}{n^3}}-1\right )$](/mathtex/c4/c4ddfdae7d77b55f091872faebc8fcc2.gif)
![kopírovat do textarea $\large\lim_{p\to\infty}\left (\lim_{n\to\infty}\sum_{k=1}^{n}\left (\sqrt{1+\frac{k}{n^2}}+\sqrt[3]{1+\frac{k^2}{n^3}}+\cdots +\sqrt[p]{1+\frac{k^{p-1}}{n^p}}+\sqrt[p+1]{1+\frac{k^p}{n^{p+1}}}-p\right )\right )=\nl =\lim_{p\to\infty}\left (\lim_{n\to\infty}\sum_{k=1}^{n}\left (\sqrt{1+\frac{k}{n^2}}-1\right)+\lim_{n\to\infty}\sum_{k=1}^n\left(\sqrt[3]{1+\frac{k^2}{n^3}}-1\right)+\cdots +\lim_{n\to\infty}\sum_{k=1}^n\left(\sqrt[p]{1+\frac{k^{p-1}}{n^p}}-1\right)+\lim_{n\to\infty}\sum_{k=1}^n\left(\sqrt[p+1]{1+\frac{k^p}{n^{p+1}}}-1\right)\right). $](/mathtex/c7/c7362274cad2c83e1aa54cc6460c1f4a.gif)
![kopírovat do textarea $ \large L_s:=\lim_{n\to\infty}\sum_{k=1}^n\left(\sqrt[s]{1+\frac{k^{s-1}}{n^s}}-1\right)=\lim_{n\to\infty}\sum_{k=1}^n\left(\left(1+\frac{k^{s-1}}{n^s}\right)^{\frac 1s}-1\right)=\nl =\lim_{n\to\infty}\sum_{k=1}^n\left(\frac 1s\,\frac{k^{s-1}}{n^s}+\frac 1s\,(\frac 1s-1)\,\frac 1{2!}\,\frac{k^{2s-2}}{n^{2s}}+\frac 1s\,(\frac 1s-1)\,(\frac 1s-2)\,\frac 1{3!}\,\frac{k^{3s-3}}{n^{3s}}+\frac 1s\,(\frac 1s-1)\,(\frac 1s-2)\,(\frac 1s-3)\,\frac 1{4!}\,\xi^4\right)=\nl =\lim_{n\to\infty}\left(\frac 1{sn^s}\,\sum_{k=1}^n k^{s-1}+\frac 1{sn^{2s}}\,(\frac 1s-1)\,\frac 1{2!}\,\sum_{k=1}^n k^{2s-2}+\frac 1{sn^{3s}}\,(\frac 1s-1)\,(\frac 1s-2)\,\frac 1{3!}\,\sum_{k=1}^n k^{3s-3}+\frac 1{s}\,(\frac 1s-1)\,(\frac 1s-2)\,(\frac 1s-3)\,\frac 1{4!}\,\sum_{k=1}^n \xi^{4}\right),\nl0\,<\,\xi\,<\,\frac{k^{s-1}}{n^s}. $](/mathtex/54/545d754cb9025062b0e49564c11fa675.gif)
 , pro
, pro  ,
, 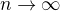 (k důkazu stačí použít Stolzovu větu nebo se podívat na
(k důkazu stačí použít Stolzovu větu nebo se podívat na 

 .
.![kopírovat do textarea $ \large\lim_{p\to\infty}\left (\lim_{n\to\infty}\sum_{k=1}^{n}\left (\sqrt{1+\frac{k}{n^2}}-1\right)+\lim_{n\to\infty}\sum_{k=1}^n\left(\sqrt[3]{1+\frac{k^2}{n^3}}-1\right)+\cdots +\lim_{n\to\infty}\sum_{k=1}^n\left(\sqrt[p]{1+\frac{k^{p-1}}{n^p}}-1\right)+\lim_{n\to\infty}\sum_{k=1}^n\left(\sqrt[p+1]{1+\frac{k^p}{n^{p+1}}}-1\right)\right)=\nl =\large\lim_{p\to\infty}\left (\frac 14+\frac 19+\cdots+\frac 1{p^2}+\frac 1{(p+1)^2}\right)=\frac{\pi^2}{6}-1. $](/mathtex/00/00fab69a0197273812f21e2e8f29bc81.gif)