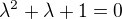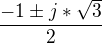Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rekurentní rovnice. (TOTO TÉMA JE VYŘEŠENÉ)
#2 15. 03. 2010 20:14
#5 15. 03. 2010 22:22 — Editoval pietro (15. 03. 2010 22:30)
Re: Rekurentní rovnice.
↑ Frantik88: obecne reseni bez prave strany: pretoze sa jedna o komplexne korene bude tam linaearna kombinace (r^n)*sin(n*uhol) a (r^n)*cos( dtto), kde
r=abs hodnota korenov = odmoc( real^2 +imag^2) = 1, uhol = arctg( imag/ real) = -pi/3.....
y(n)= c1* (1^n)* cos( n*-pi/3) + c2 * (1^n)* sin ( n*-pi/3) .. zjednodusit sa da lebo (1^n) =1,....
y(n)= c1* cos( n*-pi/3) + c2 * sin ( n*-pi/3), a teraz odhad riesenia s pravou stranou... ale neviem to zatial najst.. :(
nieco podobne http://www.math.muni.cz/~vopatova/dfile … fc-rce.pdf
http://www.math.muni.cz/~pribylova/sbirky/15.png
http://www.math.muni.cz/~pribylova/sbirky/16.png
ale nie je to prave orechove....
Offline
#6 15. 03. 2010 23:47
Re: Rekurentní rovnice.
↑ Frantik88: .....no nedari sa ..pomozte odbornici na diferencne rovnice !!!! HELP !!!
Offline
#7 16. 03. 2010 00:25
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Rekurentní rovnice.
Ten argument mi vychází 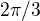 . Bez pravé strany tak máme řešení
. Bez pravé strany tak máme řešení  , pravá strana nám ke kořenům charakteristického polynomu přidá 2 a 1. Hledáme tak řešení ve tvaru
, pravá strana nám ke kořenům charakteristického polynomu přidá 2 a 1. Hledáme tak řešení ve tvaru 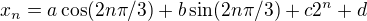 . Dosazením hned vidíme, že d=1/3, c spočteme také celkem snadno.
. Dosazením hned vidíme, že d=1/3, c spočteme také celkem snadno.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Rekurentní rovnice. (TOTO TÉMA JE VYŘEŠENÉ)
 . A nejak si nevim rady, jak vubec zacit.
. A nejak si nevim rady, jak vubec zacit.