Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 03. 2010 22:11
Explicitní vzorec
Ahoj, mám úlohu:
Pomocí vytvořujících funkcí najděte explicitní vzorec pro sumu: 1^2 + 2^2 + 3^2 + ... + n^2.
Ten vzorec samozřejmě znám, neb se dá odvodit jiným způsobem / najít v literatuře, avšak nevím, jak mám k němu přijít přes vytvořující funkce.
Můj dosavadní postup je takový, že jsem si odvodil vyt. funkci pro posloupnost lichých čísel, tj. (2/((1-x)^2) - 1/(1-x), a tu jsem vynásobil 1/(1-x), čímž jsem dostal posloupnost částečných součtů 1, 1 + 3, 1 + 3 + 5 ..., která svými hodnotami odpovídá prvkům sumy druhých mocnin čísel, kterou chci počítat.
A tak bych potřeboval poradit, jak z tohoto stadia získat explicitní vzorec. Pokoušel jsem se použít postup pro odvození explicitního vzorce pro n-té Fibbonnacciho číslo, ale skončil jsem u hrozného paskvilu, který nikam nevedl. (Možná jsem ale pouze někde udělal chybu.)
Nemá někdo v tomto směru nápad? A nebo mám zvolit jiný postup?
Díky za odpověď.
V.
Offline
- (téma jako vyřešené označil(a) awm1)
#2 29. 03. 2010 22:49 — Editoval petrkovar (29. 03. 2010 22:50)
Re: Explicitní vzorec
↑ awm1:Je to úloha 10.2.4, Kapitoly z diskrétní matematiky od Matouška a Nešetřila.
Vytvořující funkce posloupnosti samých jedniček je 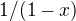 . Její DERIVACE (toto je fajn trik!) je vytvořující funkce posloupnosti
. Její DERIVACE (toto je fajn trik!) je vytvořující funkce posloupnosti 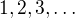 ,
,  -tý člen je
-tý člen je  .
.
Druhá derivace je vytvořující funkce posloupnosti 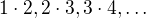 .
.  -tý člen je
-tý člen je 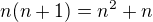 .
.
Aha! Nyní stačí od vytvořující funkce posloupnosti 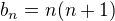 odečíst vytvořující funkci posloupnosti
odečíst vytvořující funkci posloupnosti  .
.
Alternativně můžeme tu první derivace nejprve vynásobit  a teprve potom derivovat podruhé.
a teprve potom derivovat podruhé.
Offline
#3 29. 03. 2010 22:59
Re: Explicitní vzorec
Děkuji za pomoc, avšak toto je jen alternativní přístup k určení posloupnosti druhých mocnin (tu úlohu jsem si našel a moje odvození jí odpovídá). Já bych potřeboval vědět, jak mám od té vytvořující funkce odvodit explicitní vzorec pro výpočet n-tého členu - tj. 1/6(2n^3+3n^2+n).
Offline
#4 31. 03. 2010 21:44 — Editoval Olin (31. 03. 2010 21:45)
Re: Explicitní vzorec
Chápu tedy správně, že máš vytvořující funkci pro posloupnost 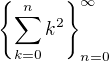 , a chceš z této vytvořující funkce zjistit předpis pro obecný člen této posloupnosti?
, a chceš z této vytvořující funkce zjistit předpis pro obecný člen této posloupnosti?
Offline
