Matematické Fórum

matoxy · 12. 02. 2008 21:20

Mal by som taký dotaz, je to príklad z Astronomcikej olympiády. Máme zisti? ako sa zmení rotácia hviezdy ak sa zmení jej plomer z $r_1$ na $r_2$ . Máme tiež danú teraz jej rotačnú periódu a hmotnos? hviezdy. Máme uvažova?, že hviezdy sa zmenší bez úniku hmoty. Mňa napadlo rieši? to napr. z energetického hľadiska. Sústavu si zvolíme tak, aby sme mali Potenciálnu energiu nulovú a potom nám ostáva teda iba zmena kinetickej energie. Tú určíme pre otáčaví pohyb a pre guľu pomocou momentu zotrvačnosti, ak ma však pamä? neklame tak ten vz?ah platí iba pre guľu s rovnomerne rozloženou hmotou. Existoval by teda nejaký spôsob ako spočíta? moment hybnosti hviezdy?

thriller · 13. 02. 2008 10:02

myslim, ze by se to melo resit pomoci zachovani momentu hybnosti, tedy toho zakona, ktery popisuje vsemi ucebnicemi otrepanou krasobruslarku, jejiy rotace se zrychluje/zpomaluje podle toho, jak odtahuje ruce od tela..

thriller

A moment hybnosti koule se pocita jako soucin momentu setrvacnosti I a uhlove rychlosti omega $L=I \omega$ $I = \frac25 m r^2$ m..hmotnost, r.. polomer koule

jelena · 13. 02. 2008 10:30

↑ thriller:

Zdravim, ve vsem mas pravdu, ale koleguv dotaz se tyka zrejme takove situace, kdy nemuze uvazovat stejnou hustotu v celem telese. Asi ta zmena hustoty musi byt podchycena dalsim integralem, ale zatim nemam nejaky rozumny napad (dopoledne :-)

thriller · 13. 02. 2008 11:28

Takze, pokusim se napsat svuj napad.

Koule ma polomer R, zavadim svericke souradnice, tak jak je to na obrazku

Moment setrvacnosti se pocita jako $I = \int_V r^2 \varrho dV$ kde r je vzdalenost od osy rotace $r = r' sin \theta$

Nyni uvazuju hustotu ne jako konstantni v celem objemu, ale jako funkci zavislou na vzdalenosti r' od stredu koule (obecnejsi by byla zavislost hustoty nejen na vzdalenosti od stredu ale i na uhlech fi a theta, ale u hvezdy mi prijde ta aproximace ujdouci) $\varrho = \varrho(r')$

Pro objemovy element v sverickych souradnicich plati (to je podle vety o substituci myslim) $dV = r'^2 sin \theta dr' d \varphi d \theta$

A ted samotny vypocet: $I = \int_V r^2 \varrho (r') dV = \int_0^R \int_0^{2 \pi} \int_0^{\pi} r'^4 sin^3 \theta \varrho (r') dr' d \varphi d \theta = \frac83 \pi \int_0^R r'^4 \varrho (r') dr'$

Dalsi vypocet yavisi na tvaru funkce ro(r'), je/li konstantni, pak vysledek vyjde $\frac83 \pi \frac{R^5}{5} \varrho = \frac83 \pi \frac{R^5}{5} \frac{3m}{4 \pi R^3} = \frac25 m R^2$ ,coz povazuji za kontrolu toho, ze to doposud bylo dobre.

thriller

funkce hustot, ktery lze dosazovat do integralu pro I, jsou napriklad takove:

1)linearni zavislost hustoty na vzdalenosti od stredu hvezdy
$\varrho (r') = \varrho_1 + \frac{\varrho_2-\varrho_1}{R} r'$

2)exponencialni zmensovani se hustoty se vzdalenosti od stredu hvezdy
$\varrho (r') = \varrho_1 e^{-Kr'}$ kde $K=\frac1R \ln \frac{\varrho_2}{\varrho_1}$

3)hyperbolicke klesani (neco jako neprima umera mezi vydalenosti a hustotou)
$\varrho (r') = \frac{\varrho_1 K}{r'+K}$ kde $K=\frac{R \varrho_2}{\varrho_1-\varrho_2}$

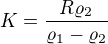
4)konstantni hodnota hustoty v urcitych slupkach
$\varrho (r') = \varrho_1 \, \forall r' \in <0, R_1>$
$\varrho (r') = \varrho_3 \, \forall r' \in <R_1,R_2>$
...
$\varrho (r') = \varrho_2 \, \forall r' \in <R_i,R>$

Vsechny tyto zavislosti jsou ukazane v obrazku: v uvadenem poradi: 1)zelena, 2)modra, 3)cervena, 4)seda

thriller · 13. 02. 2008 12:06

Ale pocitat ty integraly nebudu.

Zajimalo by me, jake jsou realne hustoty hvezd, Nevite nekdo?

matoxy · 13. 02. 2008 16:31

U neutrónovej hviezdy je tá hustota natoľko veľká, že za kávovú ližčku by vážilo toľko ako celá Zem a u slnka je priemerná hustota teraz neviem presne aká no viem, že ju nemôžné (za predpokladu správneho výsledku) použi?. Som skúšal počíta? hmotnos? Slnka tak že som spočítal objem Slnka ako gule a potom to vynásobil hustotou no vyšla tam veľká odchýlka. To ako sa mení hustota hviezdy od vzdialenosti od stredu teraz neveim no do zajtra by som možno zistil.
+ V každom prípade sa mi zdá, že to riešenie bude dos? komplikované a moje mat. schopnosti zatiaľ k takým metódam ako sú hore používané veľmi nesiahajú. Ak by som teda mohol poprosi? keď bude písa? niekdo riešenie, resp. návrh bolo by možné tie integrály vysvetli? aj slovne? Napr. toto znamená, že sa mení objem podľa takejto závyslosti, alebo niečo v tom zmysle.

Ďakujem Martin

thriller · 13. 02. 2008 17:20

Ja sem to hledal na wikipedii a tam (nejen tam) rozdělují slunce na tři části:

jádro 0-0,2R
radiační zóna 0,2R-0,7R
a ještě jedna zóna (nepamatuji) 0,7R-R

kde R je poloměr slunce.

K tomu jádru uvádějí hustotu 150 000 kgm-3. Ke zbylým dvoum zónám se mi hustotu nepodařilo najít, ale průměrná hustota slunce vypočítatelná z objemu a hmotnosti se uvádí 1400 kgm-3.

thriller

S využitím toho, co tu bylo psáno v příspěvcích #5,6 a 9 bude moment setrvačnosti I slunci-podobné hvězdy následující

$I = \frac{8}{15} \pi [\varrho_1 R_1^5 + \varrho_2 (R_2^5-R_1^5) +\varrho_3 (R_3^5-R_2^5)] = \frac25 [m_1 R_1^2 +m_2(R_2^2-R_1^2)+m_3(R_3^2-R_2^2)] = I_1 +I_2 +I_3$

kde význam použitých symbolů by měl být zřejmý z příspěvku 9 a z obrázku (viz níže), v krátkosti R_i je poloměr , ro_i je hustota a m_i je hmotnost příslušné slupky hvězdy.

Při změně poloměru hvězdy(smrš?ování či rozpínání hvězdy) se budou měnit dílčí poloměry slupek i jejich hustoty (hmotnosti slupek můžeme uvažovat neměnné), což celkem zkomplikuje použití věty o zachování momentu setrvačnosti, která má tvar

$I^{(1)} \omega^{(1)} = I^{(2)} \omega^{(2)}$ kde na levé straně jsou moment setrvačnosti a úhlová rychlost před změnou poloměru hvězdy a na druhé straně stejné veličiny po změně hvězdy.
Na první pohled je zřejmé, že zmenší-li hvězda svůj poloměr (tj. zmenší se poloměry jednotlivých slupek) zmenší se celkový moment setrvačnosti a tím pádem se zvětší úhlová rychlost a naopak.

thriller · 13. 02. 2008 18:09

Pokračuji dál v úvaze:

Vezmeme-li v úvahu, že platí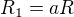
$R_1 = aR$
$R_2 = bR$
$R_3 = R$

kde R je poloměr slunci-podobné hvězdy tedy to, co lze pozorovat a koeficienty a,b jsou ta čísla 0,2 a 0,7 z příspěvku #9,tak vzorec pro moment setrvačnosti přejde v tvar
$I = \frac25 [m_1 a^2 +m_2 (b^2-a^2) +m_3(1-b^2)] R^2$

a za předpokladu, že koeficienty a a b stejně jako hmotnosti slupek m_i hvězdy zůstanou při smrš?ování/rozpínání nezměněny přejde zákon zachování na přijatelnější tvar
$R^{(1)2} \omega^{(1)} = R^{(2)2} \omega^{(2)}$ kde na levé straně jsou pozorovatelný poloměr hvězdy a její úhlová rychlost před změnou a na pravé straně po změně.

Je tedy vidt mimo jiné např. to, že dostaneme stejný výsledek, jako kdybychom počítali s průměrnou hustotou hvězdy použitím vzorečků v #3 a nezabývali se vnitřní strukturou hvězdy. Ale jsem rád, že jsme se zabývali, protože ráno jsem si to jenom myslel, teď to mám dokázané.

Prosím reakce.

matoxy · 14. 02. 2008 15:13 — Editoval matoxy (22. 02. 2008 17:31)

Nie som si celkom istý, či by čísla a,b mohli by? rovnaké aj po zmenšení hviezdy na neutrónovú pretože aj keď by hmotnos? stĺpkou zostala rovnaká priblížili by sa bližšie a z gravitačného zákona by pôsobili väčšou silou, čo by malo za následok väčší tlak. Avšak možno by to bolo kompenzované protitlakom žiarenia, či zvýšenia pohybu častíc vo vnútri neutrónovej hviezdy, no to si už nie som istý. V každom prípade nemyslím, že by to výsledok zmenilo až na toľko, aby to už aj pri tejto zložitosti malo zmysel písa? do riešenia domáceho kola AO. K tým výpočtom pred tým ešte možno budem ma? otázky no až sa na to cez výkend pozriem doma.

Ešte k tomu, že sa ukázala platnos? vz?ahu $R_1 ^2 \omega_1=R_2 ^2 \omega_2$ Ak som správne pochopil tak by tento vz?ah mal plati? aj ak by sa hustota hviezdy menila napr. nepriamo úmerne vzdialenosti. Pretože by sa to dalo zapísa? ako nekonečne veľa kruhových výsekov s nekonečne malým polomerom, pričom pre každý by prislúchala o trocha iná hustota ako pre ten predchádzajúci.

matoxy · 22. 02. 2008 17:33

Akosi som sa k tomu dostal až teraz no aj tak by som bol rád ak by si mi ešte podrobnejšie vysvetlil ako si došiel ktomuto vz?ahu: $I = \frac{8}{15} \pi [\varrho_1 R_1^5 + \varrho_2 (R_2^5-R_1^5) +\varrho_3 (R_3^5-R_2^5)] = \frac25 [m_1 R_1^2 +m_2(R_2^2-R_1^2)+m_3(R_3^2-R_2^2)] = I_1 +I_2 +I_3$ ?
ďakujem

Matematické Fórum

#1 12. 02. 2008 21:20

Rotácia hviezdy

#2 13. 02. 2008 10:02

Re: Rotácia hviezdy

#3 13. 02. 2008 10:06 — Editoval thriller (13. 02. 2008 10:07)

Re: Rotácia hviezdy

#4 13. 02. 2008 10:30

Re: Rotácia hviezdy

#5 13. 02. 2008 11:28

Re: Rotácia hviezdy

#6 13. 02. 2008 12:02 — Editoval thriller (13. 02. 2008 12:04)

Re: Rotácia hviezdy

#7 13. 02. 2008 12:06

Re: Rotácia hviezdy

#8 13. 02. 2008 16:31

Re: Rotácia hviezdy

#9 13. 02. 2008 17:20

Re: Rotácia hviezdy

#10 13. 02. 2008 17:52 — Editoval thriller (13. 02. 2008 17:57)

Re: Rotácia hviezdy

#11 13. 02. 2008 18:09

Re: Rotácia hviezdy

#12 14. 02. 2008 15:13 — Editoval matoxy (22. 02. 2008 17:31)

Re: Rotácia hviezdy

#13 22. 02. 2008 17:33

Re: Rotácia hviezdy

Zápatí