Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Konvergence nekonečné řady (TOTO TÉMA JE VYŘEŠENÉ)
#1 09. 04. 2010 11:56
Konvergence nekonečné řady
Předpokládejme, že nekonečná řada nezáporných čísel 
konverguje k hodnotě  . Dokažte, že pak konverguje i nekonečná řada
. Dokažte, že pak konverguje i nekonečná řada
Označme součet této řady symbolem 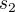 . Najděte nějaký horní odhad pro číslo
. Najděte nějaký horní odhad pro číslo 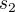 pomocí čísla
pomocí čísla  .
.
Offline
- (téma jako vyřešené označil(a) Marian)
#2 09. 04. 2010 15:25 — Editoval Pavel (09. 04. 2010 15:44)
Re: Konvergence nekonečné řady
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 09. 04. 2010 16:59 — Editoval Marian (09. 04. 2010 17:09)
Re: Konvergence nekonečné řady
Offline
#4 09. 04. 2010 17:33
Re: Konvergence nekonečné řady
Offline
#5 09. 04. 2010 17:49 — Editoval BrozekP (09. 04. 2010 17:55)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konvergence nekonečné řady
↑ Stýv:
Přesně tak, uvedu příklad: , řada tedy konverguje a přitom pro libovolně velké
, řada tedy konverguje a přitom pro libovolně velké  najdu
najdu  takové, že
takové, že  .
.
Offline
#6 09. 04. 2010 18:48
Re: Konvergence nekonečné řady
↑ Stýv:↑ BrozekP:
Konvergence plyne i z C-S, ten odhad byl zbytečný u Pavla. Myslím, že by to šlo napravit tak, že pro konvergentní nekonečné řady  s kladnými členy platí
s kladnými členy platí  pokud
pokud 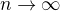 .
.
Offline
#7 09. 04. 2010 19:02
Re: Konvergence nekonečné řady
↑ Stýv:, ↑ BrozekP:
Už to vidím, máte pravdu. Tak to zkusme jinak. Nechť  je nezáporná posloupnost, pro kterou platí, že
je nezáporná posloupnost, pro kterou platí, že 
konverguje. Odsud vyplývá, že  . Rozdělme členy posoupnosti do dvou disjunktních množin:
. Rozdělme členy posoupnosti do dvou disjunktních množin: a
a  .
.
Protože se jedná o posloupnost obsahující nezáporné členy, mohu psát .
.
Protože řada na levé straně konverguje, musí také konvergovat obě řady na straně pravé.
1. Nechť  konverguje. Pak
konverguje. Pak
Tzn. řada konverguje.
konverguje.
2. Nechť  konverguje. Protože pro dostatečně velká
konverguje. Protože pro dostatečně velká  platí, že
platí, že  (viz limita nahoře), můžu psát
(viz limita nahoře), můžu psát
Opět ze srovnávacího kritéria vyplývá, že také řada
konverguje.
Tzn. konverguje také řada  .
.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 09. 04. 2010 20:53
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Konvergence nekonečné řady
Marian napsal(a):
Myslím, že by to šlo napravit tak, že pro konvergentní nekonečné řady
s kladnými členy platí
pokud
.
To neplatí, mohl bych přece uvést stejný protipříklad. Limita by neexistovala.
Offline
#9 09. 04. 2010 22:07
Re: Konvergence nekonečné řady
↑ BrozekP:
Marian chcel asi napísať, že z konvergencie  vyplýva
vyplýva  pre
pre 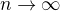 . Ale to je asi mierne od veci.
. Ale to je asi mierne od veci.
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
#10 10. 04. 2010 13:51 — Editoval Marian (10. 04. 2010 13:52)
Re: Konvergence nekonečné řady
↑ BrozekP:
Ano, zapomněl jsem předpoklad o monotonii posloupnosti {a_n}. Ale tady o monotonii v zadání není řeči. To už si pletu s jinou úlohou.
↑ lukaszh:
Toto jsem nechtěl tvrdit.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Konvergence nekonečné řady (TOTO TÉMA JE VYŘEŠENÉ)
 ,
,  platit, že
platit, že![kopírovat do textarea $ \Large a_n\,<\,\frac 1n\qquad\Rightarrow\qquad \sqrt[4]{a_n}\,<\,\frac 1{n^{1/4}}\qquad\Rightarrow\qquad \frac{\sqrt[4]{a_n}}{n^{1/2}}\,<\,\frac 1{n^{3/4}}\qquad\Rightarrow\qquad \frac{\sqrt{a_n}}{n}\,<\,\frac 1{n^{3/2}}\,, $](/mathtex/3b/3b543c545ed7f0147b73743feb059d46.gif)


 nerovnost
nerovnost


 plyne okamžitě nerovnost
plyne okamžitě nerovnost  aniž by bylo nutné použít čtvrtou odmocninu.
aniž by bylo nutné použít čtvrtou odmocninu.  "pro všechna velká n" se mi moc nezdá
"pro všechna velká n" se mi moc nezdá