Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 20. 04. 2010 21:44
- ondrej.hav
- Příspěvky: 162
- Reputace: 4
Logaritmus
Pěkný den, mám takový zvláštní dotaz... Když mám funkci 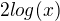 Tak jeho definiční obor by měl být vsechny kladný reálný čísla.... to bych taky normálně řekl... Ale dneska sem přemýšlel o větách o logaritmech a
Tak jeho definiční obor by měl být vsechny kladný reálný čísla.... to bych taky normálně řekl... Ale dneska sem přemýšlel o větách o logaritmech a 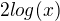 můžu napsat jako
můžu napsat jako 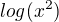 Podle nějakých vět o logaritmech... A taková funkce by měla definiční obor
Podle nějakých vět o logaritmech... A taková funkce by měla definiční obor  ;
;
Offline
- (téma jako vyřešené označil(a) ondrej.hav)
#2 20. 04. 2010 22:31 — Editoval frank_horrigan (20. 04. 2010 22:41)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Logaritmus
↑ ondrej.hav:
Takova fce ma opravdu definicni obor R-0 :) jenomze taky fce log(x) a 2log(x) jsou uplne jine. Proto, kdyz kreslis/nechavas vykreslit graf, mej to ve formatu y= 1*log(x^a), abys dostal spravny definicni obor :) Jinak, dobre kreslitko grafu tady: http://rechneronline.de/function-graphs/
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#3 20. 04. 2010 22:56
Re: Logaritmus
↑ ondrej.hav:
Ono je to tak - v reálných číslech platí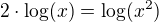
tehdy, když jsou výrazy na obou stranách definovány - tedy pokud je x>0.
Funkce 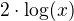 má tedy definiční obor
má tedy definiční obor  a na celém svém definičním oboru se rovná funkci
a na celém svém definičním oboru se rovná funkci 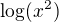 . Funkce
. Funkce 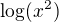 má definiční obor
má definiční obor  .
.
Offline