Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Derivace funkce (TOTO TÉMA JE VYŘEŠENÉ)
#2 21. 04. 2010 15:19 — Editoval Pavel (21. 04. 2010 16:21)
Re: Derivace funkce
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#3 23. 04. 2010 13:54
Re: Derivace funkce
↑ Pavel:
Ano, je to jedna z možností.
Dá se postupovat ovšem i tak, že lze psát
Odtud podle věty o derivaci složené funkce lze najít výsledek podobně, neboť na levé straně dostaneme
Váhal jsem, zda-li úloha nepatří do sekce zajímavých úloh pro střední školu.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematické analýzy
- » Derivace funkce (TOTO TÉMA JE VYŘEŠENÉ)


 a
a  značí inverzní funkci.
značí inverzní funkci. je funkce spojitá a prostá na intervalu
je funkce spojitá a prostá na intervalu 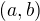 . Pak
. Pak  a platí
a platí
 . Pak
. Pak
