Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Dukaz vlastnosti korenu polynomu (TOTO TÉMA JE VYŘEŠENÉ)
#1 02. 05. 2010 16:00 — Editoval rutt (04. 05. 2010 19:47)
Dukaz vlastnosti korenu polynomu
cuzz, mam polynom 
za predpokladu  dokazte, ze
dokazte, ze  .
.
myslela jsem, ze bude stacit to roznasobit, ziskat 4 rovnice:
a ze z toho vyleze nakej jasnej zlomek, nebo pripadne, ze do toho jeste dosadim za  , kde
, kde  , ale nak to nevyslo.. nemel by tu nekdo napad? celkem to hori.
, ale nak to nevyslo.. nemel by tu nekdo napad? celkem to hori.
Offline
- (téma jako vyřešené označil(a) rutt)
#2 02. 05. 2010 16:09
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dukaz vlastnosti korenu polynomu
Nezapomněla jsi na něco? Obecně to totiž nejde dokázat. Nemají být koeficienty  třeba racionální? Tady je protipříklad:
třeba racionální? Tady je protipříklad:
Offline
#3 02. 05. 2010 16:16
Re: Dukaz vlastnosti korenu polynomu
↑ BrozekP:
nezapomnela, ale mozna na to zapomnela ucitelka, klidne to vem jako predpoklad, jestli myslis, ze by ta uloha mela byt takhle zadana a jinak ji nema smysl resit.
Offline
#4 02. 05. 2010 18:16
#5 03. 05. 2010 16:50
Re: Dukaz vlastnosti korenu polynomu
hele staci i nakej napad, jak zacit. celkem to specha://
myslim, ze 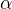 a
a  by mely byt obe racionalni, aby
by mely byt obe racionalni, aby  , co se tyce toho soucinu, tak tam muzou byt bud obe racionalni, nebo obe iracionalni, aby z jejich nasobku vzeslo racionalni cislo, ale to uz je asi jedno. takze jde vlastne asi o to dokazat, ze alfa a beta jsou racionalni.
, co se tyce toho soucinu, tak tam muzou byt bud obe racionalni, nebo obe iracionalni, aby z jejich nasobku vzeslo racionalni cislo, ale to uz je asi jedno. takze jde vlastne asi o to dokazat, ze alfa a beta jsou racionalni.
Offline
#6 03. 05. 2010 17:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dukaz vlastnosti korenu polynomu
↑ rutt:
Pravděpodobně nepotřebujeme dokazovat, že  a
a  jsou obě racionální (nejspíš to ani neplatí).
jsou obě racionální (nejspíš to ani neplatí).
Z první rovnice plyne, že součet  je racionální číslo. Jsou tedy dvě možnosti
je racionální číslo. Jsou tedy dvě možnosti
1)  jsou obě racionální. Pak je i
jsou obě racionální. Pak je i  racionální a z druhé rovnice okamžitě plyne, že i
racionální a z druhé rovnice okamžitě plyne, že i  je racionální, což jsme měli dokázat.
je racionální, což jsme měli dokázat.
2)  jsou obě iracionální (o jejich součinu ale zatím nic nevíme). Jsou opět dvě možnosti
jsou obě iracionální (o jejich součinu ale zatím nic nevíme). Jsou opět dvě možnosti
2A)  je racionální. Pak z druhé rovnice plyne, že
je racionální. Pak z druhé rovnice plyne, že  je racionální.
je racionální.
2B)  je iracionální. Z poslední rovnosti by plynulo, že
je iracionální. Z poslední rovnosti by plynulo, že  je iracionální. Pokud tvrzení, které dokazujeme, opravdu platí, pak tento případ zřejmě nemůže nastat. Nenapadá mě ale, jak to ukázat.
je iracionální. Pokud tvrzení, které dokazujeme, opravdu platí, pak tento případ zřejmě nemůže nastat. Nenapadá mě ale, jak to ukázat.
Offline
#7 03. 05. 2010 19:17 — Editoval rutt (03. 05. 2010 19:18)
Re: Dukaz vlastnosti korenu polynomu
↑ BrozekP:
tak to byly dva skutecne dementni dotazy (rovnou jsem je smazala). kazdopadne dik za skoro kompletni reseni.
hele a nemuze to, ze gama*delta nesmi byt iracionalni nak plynout z ty posledni rovnice a toho, ze alfa+beta!=gama+delta?
Offline
#8 03. 05. 2010 20:04
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dukaz vlastnosti korenu polynomu
↑ rutt:
Možná to není skoro kompletní řešení, třeba je to slepá ulička, to se takhle nedá říct.
Nevím, proč by z poslední rovnice a z  mělo plynout, že
mělo plynout, že  je racionální. Můžeš být konkrétnější?
je racionální. Můžeš být konkrétnější?
Offline
#9 03. 05. 2010 20:29 — Editoval BrozekP (03. 05. 2010 20:29)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dukaz vlastnosti korenu polynomu
Tak kompletní řešení:
Z první rovnice plyne  . Z druhé pak
. Z druhé pak  . Do levé strany třetí rovnice dosadím za
. Do levé strany třetí rovnice dosadím za  :
:![kopírovat do textarea $\alpha\beta(\gamma+\delta)+(\alpha+\beta)(p-\alpha\beta)=\alpha\beta[(\gamma+\delta)-(\alpha+\beta)]+(\alpha+\beta)p$](/mathtex/cd/cd17398fe84874ee35a72a9e9db2e370.gif)
Tento výraz je roven racionálnímu číslu. Protože  je racionální číslo, hranatá závorka je různá od nuly a přitom racionální, musí být i
je racionální číslo, hranatá závorka je různá od nuly a přitom racionální, musí být i  racionální.
racionální.
Offline
#10 03. 05. 2010 20:41
#11 05. 05. 2010 16:15 — Editoval Marian (05. 05. 2010 16:17)
Re: Dukaz vlastnosti korenu polynomu
Třetí rovnice by se mohla vynásobit ještě číslem  . Označím-li
. Označím-li 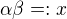 , dostanu kvadratickou rovnici v "x" s racionálními koeficienty (využívám u toho čtvrtou rovnici). Tady by diskuze mohla pokračovat, neboť zde dostaneme, že diskrimainant kvadratické rovnice je čtverec tehdy a jen tehdy, když
, dostanu kvadratickou rovnici v "x" s racionálními koeficienty (využívám u toho čtvrtou rovnici). Tady by diskuze mohla pokračovat, neboť zde dostaneme, že diskrimainant kvadratické rovnice je čtverec tehdy a jen tehdy, když  je racionální.
je racionální.
Ovšem tvůj dodatečný postup je elegantní a vyhne se kvadratické rovnici a dalším diofantickým úvahám.
Na zadání úlohy se mi příliš nelíbí fakt, že nulové body  nejsou nijak specifikovány. Mělo by se tedy dokázat, že tvrzení platí pro libovolné pořadí. Narážím na předpoklad o součtech dvojic kořenů. Jak vím, který je zrovna
nejsou nijak specifikovány. Mělo by se tedy dokázat, že tvrzení platí pro libovolné pořadí. Narážím na předpoklad o součtech dvojic kořenů. Jak vím, který je zrovna  a který
a který  ? Podobně další.
? Podobně další.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Dukaz vlastnosti korenu polynomu (TOTO TÉMA JE VYŘEŠENÉ)
