Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 05. 2010 14:12 — Editoval frank_horrigan (08. 05. 2010 14:14)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Tečna kružnice
Zdravím, řeším tady s jednou kočenou mojí (a asi nejen mojí) neoblíbenou analytickou geometrii, zasek jsem se hned na zacatku (takze toho bude asi vic), ale proste nevim: Najděte rovnici tečny kružnice, která prochází bodem [-4;-2] a středem [0;0]. Rovncii kružnice jsem dal dohromady, ale s tou tečnou netuším co počítám. Myslím si, že půjdou zneužít vektory. Vím, že normálový je roven poloměru, a směrový je na něj kolmý, ale nedokážu to tam dosadit :) Díky
EDIT: ta tečna má také procházet bodem [-4;-2] :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
- (téma jako vyřešené označil(a) frank_horrigan)
#2 08. 05. 2010 14:44 — Editoval septolet (08. 05. 2010 14:51)
Re: Tečna kružnice
↑ frank_horrigan:
Rovnice kružnicev tomto případě bude: 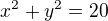
Obecná rovnice přímky je:  , kde
, kde  ,
,  jsou souřadnice normálového vektoru. Normálový vektor v tomto případě bude
jsou souřadnice normálového vektoru. Normálový vektor v tomto případě bude 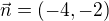 (vytvořený z bodů
(vytvořený z bodů  a
a  )
)
Dosadíme do rovnice přímky (tečny): 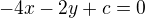 , vypočítáme
, vypočítáme  . Rovnice tečny by tedy měla být:
. Rovnice tečny by tedy měla být: 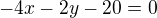 , což lze upavit do "hezčího" tvaru:
, což lze upavit do "hezčího" tvaru: 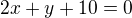 , případně to lze vyjádřit pomocí směrnicového tvaru přímky nebo pomocí parametrického tvaru.
, případně to lze vyjádřit pomocí směrnicového tvaru přímky nebo pomocí parametrického tvaru.
EDIT: "Zkoušku" lze provést tak, že vyřešíme soustavu rovnic: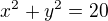
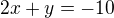
Z druhé si vyjádřím: 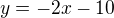 , dosadím do první rovnice, upravím:
, dosadím do první rovnice, upravím: 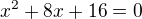 , řeším kvadratickou rovnici, diskriminant je roven 0, takže je to tečna ke kružnici
, řeším kvadratickou rovnici, diskriminant je roven 0, takže je to tečna ke kružnici 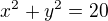 procházející bodem
procházející bodem ![kopírovat do textarea $A[-4,-2]$](/mathtex/b1/b1ad2be8888d378fadd512537ba22421.gif) .
.
Offline
#3 08. 05. 2010 14:47
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Tečna kružnice
↑ septolet:
Díky, to jsem potřeboval vědět, jak naložit s těma vektorama :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline