Matematické Fórum

Veter@n · 09. 05. 2010 20:04

Dobrý večer všem,

ve škole zrovna probíráme soustavy rovnic a jsem z toho jelen. Nechápu, kde se berou ty čísla, kterými se to násobí. Uvedu příklady, které mám mít na zítra udělané. Byl bych rád, kdyby mi někdo ke každému druhu příkladu napsal jak na něj. Budu moc rád za každou pomoc. Předěm děkuju, Lukáš.

1) 4x+3y=6
2x+y=4

2) x+15y=53
3x+y=27

3) x+4y=37
2x+5y=53

4)3x-5y=11
6x-10y=22

5)x=-3y+20
x=5y+12

6)2x+3y=1
3x+2y=9

7)12y=11x-196
12x=13y+213

8)x+y=3,5
3x+8y=22

9) 4x+3y= -4
6x+5y= -7

10) 3x-5y=14
6x-10y=17

11) 7x+3y=100
14x+6y=200

12) y=-2x+5
y=-2x -7

13) 5x +5y=3
3x-3y=5

14) 2x-3y=8
3x-2y=27

15) 2x-3y -4 = 0
3x-y -17=0

16) 2x+7y -18=4(x+y)
5x-4y-13=2(x-y)

17) (x+4).(y-2)=(x-5).(y+4)
(x+6).(y-1)=(x-1).(y+2)

18) (x+3). (y+5)=(x+1). (y+8)
(2x-3). (5y+7)= 2(5x-6). (y+1)

19)(x+5).(y-2)=(x+2).(y-1)
(x-4). (y+7)= (x-3).(y+4)

20) 5.(3x+y)-8.(x-6y)=200
20(2x-3y) -13(x-y)=520

21) 2.(x+y)-5.(y-x)=17
3.(x+2y)+7.(3x+5y)=7

22) (x+1)2 + (y+1)2 +10=x(x+6)+y(y+6)
(x+1)2 - (y+1)2 +8 = x(x-6)- y(y-6)

zdenek1 · 09. 05. 2010 20:08

↑ Veter@n:
1) druhou rovnici vynásobit dvěma a odečíst
2) první třemi, odečíst
3) první dvěma, odečíst
4) první dvěma, odečíst
5) odečíst

atd.

septolet

↑ Veter@n: Tak obecně by se dalo říct, že vždycky se snažíme zbavit nějaké proměnné a vypočítat hodnotu jiné proměnné a zpětným dosazením určit hodnotu té první proměnné.

Takže když bych ti to ukázal na prvním příkladu:

$4x+3y=6\nl 2x+y=4$

Řekněme, že se chceme zbavit nejprve proměnné $x$ , tak druhou rovnici vynásobíme $-2$ :

$4x+3y=6\nl -4x-2y=-8$

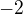Nyní je krásně vidět, že pokud obě rovnice sečteme, tak nám proměnná $x$ vypadne, tak to pojďme provést:

$y=-2$

Tím jsme dostali hodnotu proměnné $y$ , zpětně dosadíme a tím dopočítáme hodnotu proměnné $x$ :

$2x-2=4\nl 2x=6\nl x=3$

Je to trochu jasné? Zkus podobným principem spočítat ostatní příklady a kdyžtak sem napiš, kde si se zasekl a někdo ti pomůže.

frank_horrigan

Trocha teorie: máš tři možnosti (na ZS/SS tri, pak jeste nejaky matice, nebo co, sam tomu nerozumim), jak tyto soustavy řešit: Dosazení, tedy tak, že si vyjádřís z jedné rovnice x nebo y a to dosadíš do té druhé (příklad uvedu záhy)
Druhý způsob je sečtením, že jednu rovnici vynásobíš tak, aby kdyz je pak dáš do sebe (sečteš), tak ti jedna neznámá vypadla, a řešíš jako normální rovnici. Její kořen pak dosadíš do jedné z nich a vypočítáš druhou neznámou (taky ukážu). Třetí metoda, je metoda srovávací, kdy si z obou rovnic vyjdáříš tu samou neznámou a druhé strany si položíš rovny. Také, udělám ti příklad :)

EDIT: kolegové už to řeší, evidentně mají rádi tu sčítací metodu :)

Veter@n · 09. 05. 2010 20:14

Už je mi to trochu jasné. Pokusím se vypočítat nějaké příklady a ty co mi nepůjdoz napíšu sem.

teolog · 09. 05. 2010 20:18

↑ Veter@n:
V zásadě máte dvě možnosti, jak soustavy řešit (grafickou možnost teď nepočítám).

1. Metoda dosazovací: z jedné rovnice si vyjádřete jakoukoliv neznámou a dosaďte ji do druhé rovnice. Tím vypočítáte jednu neznámou a tu dosaďte opět do druhé rovnice a vypočítejte tu druhou.

2. Metoda sčítací: rovnice (nebo jednu z nich - podle potřeby) vynásobte ttakovým vhodným číslem, aby se po sečtení rovnic jedna neznáma úplně vynulovala. Tím dostanete rovnici o jedné neznámé a tu dopočítejte. Paj dosaďte do druhé rovnice a získejte druhou neznámou.

Pro názornost předvedu obě metody pro první příklad:

$4x+3y=6$
$2x+y=4$

1. metoda:
z druhé rovnice si vyjádřím např. y: $y=-2x+4$ a toto y dosadím do první rovnice: $4x+3(-2x+4)=6$
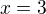dopočítám: $-2x=-6$ tedy $x=3$ a toto x dosazuji do druhé rovnice: $2*3+y=4$ a získávám y: $y=-2$

2. metoda:
Druhou rovnici vynásobím mínus trojkou, takže soustava pak vypadá takto:
$4x+3y=6$
$-6x-3y=-12$
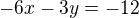
Obě rovnice sečtu a dostávám: $-2x=-6$ tedy $x=3$ .
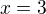Opět dosazji ya x do druhé rovnice a zjistím y.

7867088 · 09. 05. 2010 20:26

Gaussova eliminační metoda pro matice je vlastně ekvivalentní té dosazovací? A Jordanova metoda před jednotkovou matici je zase ekvivalentní té sčítací?

Veter@n · 09. 05. 2010 20:26

Děkuju moc a pomohl by mi někdo vypočítat posledních 7 příkladů.

frank_horrigan

↑ Veter@n:

Událám ti jeden, z těch těžších, ostatní jsou v podobném duchu:

19)(x+5).(y-2)=(x+2).(y-1)
(x-4). (y+7)= (x-3).(y+4)

xy-2x+5y-10 = xy-x+2y-2
xy+7x-4y-28 = xy+4x-3y-12

-2x+5y-10=-x+2y-2
7x-4y-28=4x-3y-12

-x+3y-8=0
3x-y-16=0 //EDIT: sem pak dosadím kořen, můžeš samozřejmě i na začátek, ale pak bys to musel roznásobovat znova cely, tim si usnadním práci

x= 3y-8
///////////
3(3y-8)-y-16 =0

9y-24-y-16 = 0
8y =40

y = 5

dosadím zpátky, do tý upravený: 3x-5-16 =0
3x = 21
x=7

V podobném duchu dáš i ty ostatní.. roznásob závirky a upravuj, zbav se neznámé, najdi kořen, dosaď zpátky :)

Veter@n · 09. 05. 2010 20:42

ok, akže když je počítám, tak musím to vynásobit takovým číslem, abychom je mohly odečíst

frank_horrigan · 09. 05. 2010 20:43

↑ Veter@n:

Když to jde, a je to vidět na první pohled, tak jo, tam kde to na první pohled nevidíš, nekomplikuj si život a použij substituční metodu :)

Veter@n · 09. 05. 2010 20:44

chjo, vypadá to, že to sám nezvládnu :-(

frank_horrigan

↑ Veter@n:

Neboj se toho... hele, víš co?? abych ti to spočítal celý (s čímž nemám problém) je nesmysl, protože ti to k ničemu nebude, kdyz to nepochopíš. Vyber si z lehčí z těch těžších (třeba 16), a počítej: Roznásobíš závorky (u obou rovnic). Zbav se velkých čísel a moc členů, prostě úpravy rovnice, tak aby byla jendoduchá (tvar ax+by = c, nebo ax+by-c = 0, to je jedno, jak se ti s tím bude pracovat líp, to použij). Potom, jestli pujde jedna nebo druhá (nebo obě) zkrátit, zkrať je. Budto uvidíš, čím jedna z rovnic půjde vynásobit, aby jedna z neznámých se odečetla, nebo to neuvidis. Pokud to neuvidis, tak to nehledej, a vyjádři si jednu neznámou (budeš mít tvar ax = -by +c, z toho x = (-by+c)/a). A za x dosaď do druhé rovnice... co ještě nechápeš? Klidne se ptej, vysvetlime jak umíme :)

Veter@n · 09. 05. 2010 20:50

Nemohl by mi někdo napsat, čím to vynásobit u každého příkladu. Ted tu počítám a nevím , jestli je to sčítací nebo dosazovací :-(

frank_horrigan · 09. 05. 2010 20:53

↑ Veter@n:

Tu si můžeš vybrat!! Pokud nemáš v testu přímo zadáno: najděte kořeny x, y a řešte sčítací/dosazovací/srovnávací metodou, tak si vyber. Já nerad hledám nějaký čísla, kterýma co a jak násobit, tak mám radši tu dosazovací. Má tu výhodu, ze se dá použit vzdycky, a jednoduse (coz u ty scitaci jde taky vzdycky, ale ve určitých (většine) případů ne jednoduse :)

Veter@n · 09. 05. 2010 20:53

a mohl by jsi mi je všechny vypočítat a dát je jako abych pak dal zobrazit řešení a zkusil bych to sám a pak se koukl na řešení. Potřebuji to na zítra a nechci dopadnout zle. Jestli nchceš, pochopím to. A já nejsem jeden z těch, který to bezhlavě opíše a odevzdá.

gadgetka · 09. 05. 2010 20:53

Veter@n napsal(a):
Nemohl by mi někdo napsat, čím to vynásobit u každého příkladu. Ted tu počítám a nevím , jestli je to sčítací nebo dosazovací :-(

Když ti nejde násobení, tak osamostatni z jedné rovnice jednu neznámou a dosaď ji do druhé rovnice. K řešení též dojdeš. :)

Veter@n · 09. 05. 2010 20:55

Lépe se to naučím , když to uvidím zpočítané. Potom to zkusim aplikovat na jiné příklady.

frank_horrigan · 09. 05. 2010 20:56

↑ Veter@n:

Všechny ti opravdu počítat nebudu, ale aby se o mně neřeklo, že jsem zlej, tak ti udělám ještě jeden, a krok za krokem, textově co jsem udělal,( jako na základní škole nás nutili dělat) a co máš dělat taky, jestli se to chces naucit. Steb by step, každou úpravu do vlastní hide sekce

gadgetka · 09. 05. 2010 21:09

22)
$(x+1)^2 +(y+1)^2+10=x(x+6)+y(y+6)\nl (x+1)^2-(y+1)^2+8=x(x-6)- y(y-6)$

$x^2+2x+1+y^2+2y+1+10=x^2+6x+y^2+6y\nl x^2+2x+1-y^2-2y-1+8=x^2-6x-y^2+6y$

$4x+4y=12|\cdot 2\nl8x-8y=-8$

$8x+8y=24\nl8x-8y=-8\nl16x=16\nlx=1\nly=2$

nebo:
$4x+4y=12|:4\nl8x-8y=-8|:8\nlx+y=3\nlx-y=-1\nl2x=2\nlx=1\nly=2$

jelena · 09. 05. 2010 21:12

Veter@n napsal(a):
Lépe se to naučím , když to uvidím zpočítané. Potom to zkusim aplikovat na jiné příklady.

Dej mi, prosím, vedet, až to budeš aplikovat na jiné příklady - abych tu radostnou udalost nepropasla. Zatím jsem neměla to potěšení.

Materiál (děkuji autorovi), aby se neřeklo, že to je OT a zdravím v tématu.

frank_horrigan

Vezmu si třeba 18)

18) (x+3). (y+5)=(x+1). (y+8)
(2x-3). (5y+7)= 2(5x-6). (y+1)

krok 1: roznásobit "vytknutiny"

Autor skryl část textu. Zobrazit/skrýt!

krok II. roznásobíš, každý člen polynomu s každým

Autor skryl část textu. Zobrazit/skrýt!

krok III. rovnici si zjednodušit, nechat si jedno a.x a jedno b.y

Autor skryl část textu. Zobrazit/skrýt!

krok IV: vyjádřit si z libovolné rovnice jednu neznámou:

Autor skryl část textu. Zobrazit/skrýt!

krok V. > dosadit do puvodní rovnice za x:

Autor skryl část textu. Zobrazit/skrýt!

krok VI. dopočítat lineární rovnici o jedné neznáme

krok VII: kořeen této rovnice dosadit zpátky do jedné ze soustavy a dopočítat druhý kořen.

Veter@n · 09. 05. 2010 21:27

děkuju moc, zkusím sám..:-)

Veter@n

Tak jsem tu znova, bohužel jsem ty příklady nezvládl a proto vás prosím. Nenašel by se tu někdo, kdo by mi je všechny vypočítal?
Trochu něco chápu, ale to je asi tak vše. Kamarád má s těmito soustavami také potíže a určitě by mu tyto vypočítané příklady pomohly jako vzor.
Já to lépe pochopím, když to uvidím vše vypočítané a u každého příkladu. Bohužel nemám nikoho, kdo by si semnou sedl a příklad po příkladu semnou projel. Pokud se teda najde někdo, kdo mi je vypočítá všechny, budu moc vděčný. Předem děkuju a přeji pěkný zbytek dne.

Jan Jícha · 12. 05. 2010 22:19

Vše už tu bylo řečené. Mnohé rovnice i spočítané. Jestli chceš teorii, najdeš ji například zde http://www.matweb.cz/soustavy-rovnic

Matematické Fórum

#1 09. 05. 2010 20:04

Soustavy rovnic

#2 09. 05. 2010 20:08

Re: Soustavy rovnic

#3 09. 05. 2010 20:11 — Editoval septolet (09. 05. 2010 20:13)

Re: Soustavy rovnic

#4 09. 05. 2010 20:12 — Editoval frank_horrigan (09. 05. 2010 20:14)

Re: Soustavy rovnic

#5 09. 05. 2010 20:14

Re: Soustavy rovnic

#6 09. 05. 2010 20:18

Re: Soustavy rovnic

#7 09. 05. 2010 20:26

Re: Soustavy rovnic

#8 09. 05. 2010 20:26

Re: Soustavy rovnic

#9 09. 05. 2010 20:41 — Editoval frank_horrigan (09. 05. 2010 20:42)

Re: Soustavy rovnic

#10 09. 05. 2010 20:42

Re: Soustavy rovnic

#11 09. 05. 2010 20:43

Re: Soustavy rovnic

#12 09. 05. 2010 20:44

Re: Soustavy rovnic

#13 09. 05. 2010 20:50 — Editoval frank_horrigan (09. 05. 2010 20:51)

Re: Soustavy rovnic

#14 09. 05. 2010 20:50

Re: Soustavy rovnic

#15 09. 05. 2010 20:53

Re: Soustavy rovnic

#16 09. 05. 2010 20:53

Re: Soustavy rovnic

#17 09. 05. 2010 20:53

Re: Soustavy rovnic

Veter@n napsal(a):

#18 09. 05. 2010 20:55

Re: Soustavy rovnic

#19 09. 05. 2010 20:56

Re: Soustavy rovnic

#20 09. 05. 2010 21:09

Re: Soustavy rovnic

#21 09. 05. 2010 21:12

Re: Soustavy rovnic

Veter@n napsal(a):

#22 09. 05. 2010 21:20 — Editoval frank_horrigan (09. 05. 2010 21:28)

Re: Soustavy rovnic

#23 09. 05. 2010 21:27

Re: Soustavy rovnic

#24 12. 05. 2010 21:53 — Editoval Veter@n (12. 05. 2010 21:55)

Re: Soustavy rovnic

#25 12. 05. 2010 22:19

Re: Soustavy rovnic

Zápatí