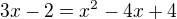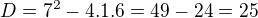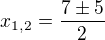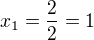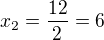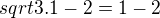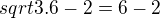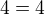Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 05. 2010 18:57
- princess21
- Příspěvky: 34
- Reputace: 0
odmocniny
dobry den, potrebovala by som aby mi niekto vysvetlil tieto dva typy prikladov, ale tak ako pre uplneho debila...ja im proste neviem prist na zub, a uz som dost nervozna z toho :( dakujem vam krasne! :)
1.
vypocitat zlomok - vysledok ma byt -1/4
(|√(2-√3) |) / (2-|1-√2|-|3-√3|)
2.zistit pocet vsetkych realnych korenov rovnice:
√(3x-2)=x-2
vysledok je 2
dufam ze to mam zrozumitelne napisane zadanie. este raz dakujem za pomoc
Offline
- (téma jako vyřešené označil(a) Doxxik)
#2 12. 05. 2010 19:31 — Editoval frank_horrigan (12. 05. 2010 20:05)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: odmocniny
↑ princess21:
Ten druhý příklad ti vysvětlím z patra, momentík, sepisuju to :)
EDIT 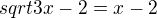 . Rovnici s odmocninou řešíš obecně řečeno tak, že si odmocninu osamostatníš na jednu stranu (obvykle levou, i kdyz je to vlastně jedno), v tomhle příkladu to už tak máš zadaný. Tedy, celou rovnici jenom umocníš na kvadrát, tím se zbavíš tý odmocniny. Vyjde tedy
. Rovnici s odmocninou řešíš obecně řečeno tak, že si odmocninu osamostatníš na jednu stranu (obvykle levou, i kdyz je to vlastně jedno), v tomhle příkladu to už tak máš zadaný. Tedy, celou rovnici jenom umocníš na kvadrát, tím se zbavíš tý odmocniny. Vyjde tedy 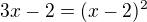 . Dál už upravuješ, až z toho vypadne normální kvadratická rovnice v normalizovaném tvaru ax^2 + bx+c =0. Konkrétní řešení ti udělám ve skrytém textu. Pozor: umocňování rovnice NENÍ ekvivalentní úprava jako je třeba odcítání nebo násobení, musíš VŽDY provést zkoušku dosazením, pokud rovnice takto nevyjde, příslušný kořen není kořenem :)
. Dál už upravuješ, až z toho vypadne normální kvadratická rovnice v normalizovaném tvaru ax^2 + bx+c =0. Konkrétní řešení ti udělám ve skrytém textu. Pozor: umocňování rovnice NENÍ ekvivalentní úprava jako je třeba odcítání nebo násobení, musíš VŽDY provést zkoušku dosazením, pokud rovnice takto nevyjde, příslušný kořen není kořenem :)
Zkouška dosazením:
Gadgetko, děkuji za upozornění, přišel jsem na to při kontrole sám, ale i přesto děkuji :)
Jestě jeden EDIT: výsledek máš dva reálné kořeny, ale mně to v té zkoušce opravdu nevychází. Druhá odmocnina z jedné se opravdu nemá rovnat -1. Nebo mi na základní škole něco uniklo?
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#4 12. 05. 2010 20:03
- princess21
- Příspěvky: 34
- Reputace: 0
Re: odmocniny
frank dakujem, teraz vidim ze je to jednoduche, len neviem preco, ja som tam stale chcela davat pod odmocninu aj tu druhu stranu...no nerozumiem co mi to napadlo...dakujem este raz :)
Offline
#5 12. 05. 2010 20:07 — Editoval frank_horrigan (12. 05. 2010 20:27)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: odmocniny
Ten první ti zkusím udělat taky, malý moment, už hodím si to na papír, abych nepolet znaménka až se budu zbavovat těch abs. hodnot :) Rozeberu si přibližné hodnoty těch odmocnin. sqrt2 je menší než 2, sqrt3 také menší než 2. Z toho vycházím a odstraním absolutní hodnoty tak, že 1-sqrt2 je záporné číslo, tak z něj udělám kladné že to otočím sqrt2-1, to je absolutní hodnota. U osatních se odčítá menší od většího, takže se toho zabvíme natvrdo:
Rozeberu si přibližné hodnoty těch odmocnin. sqrt2 je menší než 2, sqrt3 také menší než 2. Z toho vycházím a odstraním absolutní hodnoty tak, že 1-sqrt2 je záporné číslo, tak z něj udělám kladné že to otočím sqrt2-1, to je absolutní hodnota. U osatních se odčítá menší od většího, takže se toho zabvíme natvrdo: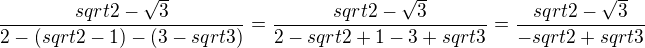
Dál už to upravit nedokážu, to by měl být výsledek... maximálně tak otočit jmenovatele (sčítání je komutativní) 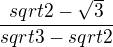
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline