Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Binomický koeficient (TOTO TÉMA JE VYŘEŠENÉ)
#2 27. 05. 2010 06:37 — Editoval check_drummer (28. 05. 2010 18:00)
- check_drummer

- Příspěvky: 4901
- Reputace: 105
Re: Binomický koeficient
(Ne vždy jsem zde důlsledný.)
"Máte úhel beta." "No to nemám."
Offline
#3 27. 05. 2010 10:01 — Editoval Pavel (27. 05. 2010 10:03)
Re: Binomický koeficient
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 28. 05. 2010 17:52 — Editoval check_drummer (28. 05. 2010 18:01)
- check_drummer

- Příspěvky: 4901
- Reputace: 105
Re: Binomický koeficient
"Máte úhel beta." "No to nemám."
Offline
#5 01. 06. 2010 14:09
Re: Binomický koeficient
↑ Marian:
Tak to je hodně pěkná úloha - řešení na dva řádky :-)
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#6 01. 06. 2010 14:30
Re: Binomický koeficient
↑ Pavel:
No jistě, gratuluju!!! Bylo to velmi snadné.
Teď už zbývá vyřešit ze zajímavých úloh limitu s aritmetickou funkcí, kde to není taky extrémně komplikované. Chystám už další úlohu, ať si procvičíme aritmetické funkce lépe.
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z diskrétní matematiky
- » Binomický koeficient (TOTO TÉMA JE VYŘEŠENÉ)

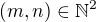 ,
, 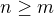 , platí
, platí
 ,
, ,
, 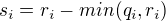 ,
, 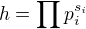 ,
, , která dříve zněla
, která dříve zněla 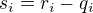 )
) jsou prvočísla
jsou prvočísla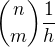 .
. je celé číslo). Zabývejme se tedy jen těmi prvočísly
je celé číslo). Zabývejme se tedy jen těmi prvočísly  dostaneme: X=n(n-1)...(n-m+1)/(m!).
dostaneme: X=n(n-1)...(n-m+1)/(m!).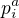 a
a 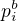 ).
).  (pro nějaké konečné K). Každý j-tý člen sumy vyjadřuje příspěvek
(pro nějaké konečné K). Každý j-tý člen sumy vyjadřuje příspěvek  -tých mocnin do výsledného exponentu.
-tých mocnin do výsledného exponentu.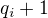 a
a  jsou splněny předpoklady T2 a těchto j je přesně
jsou splněny předpoklady T2 a těchto j je přesně  . Tedy b >= a +
. Tedy b >= a +  a
a 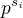 , tedy po "vykrácení" zůstane pouze v čitateli mocnina
, tedy po "vykrácení" zůstane pouze v čitateli mocnina 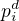 .
. ? Podobně pro
? Podobně pro  .
. .
.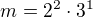 a
a 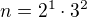 . Pak podle Tvého
. Pak podle Tvého  a
a 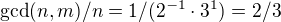 . Jenže
. Jenže 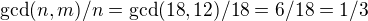 .
.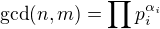 , kde
, kde 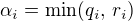 .
. , je to triviální. V ostatních případech už méně :-)
, je to triviální. V ostatních případech už méně :-) . Revize se pokusím červeně odlišit.
. Revize se pokusím červeně odlišit.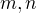 existují vždy celá čísla
existují vždy celá čísla 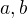 taková, že
taková, že  . Pak lze v našem případě psát
. Pak lze v našem případě psát