Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 05. 2010 09:03
Součet vlastních čísel - důkaz
Ahoj,
potřeboval bych ke zkoušce vědět, jak dokázat, že součet vlastních čísel matice odpovídá její stopě, tj. součtu jejích diagonálních prvků. Ve skriptech od pana Bečváře je pouze napsáno, že to vychází z předposledního koeficientu charakteristického polynomu dané matice, ale už nechápu proč a kvůli čemu.
Znáte někdo nějaký rozumný důkaz? Žádný jiný se mi nepodařilo najít.
Předem díky za odpověď.
V.
Offline
#2 27. 05. 2010 09:13 — Editoval BrozekP (27. 05. 2010 09:20)
- Pavel Brožek
- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Součet vlastních čísel - důkaz
(Předposledním koeficientem se myslí ten u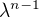 
.)
1) Zkusil bych použít Vietovy vzorce.
2) Determinant je součet přes permutace. Ale jen při jedné permutaci může vzniknout člen s 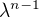- zkus ho najít.
Offline