Matematické Fórum

Ferdish · 29. 05. 2010 23:17

Zdravim, vedel by mi niekto nacrtnut dokaz tychto podmeniok? Skusal som priamy dokaz cez definicu derivacie (ako pri kartezskych), no zrejme robim chybu uz pri transformacii suradnic, resp. substitucii kompl.premennej $z=r\e(i\phi)$ , kde $r$ je modul a $\phi$ argument kompl. premennej.

Rumburak

Pro převod CR pomínek z kartéských souřadnic do polárních bych zkusil použít větu o derivaci složené funkce .
Je-li při známé licenci např. a(x,y) = Re f(x + yi) , x = r cos t, y = r sin t , potom

$\frac {\partial a}{\partial r} \,=\, \frac {\partial a}{\partial x} \,\frac {\partial x}{\partial r} \,+\, \frac {\partial a}{\partial y} \,\frac {\partial y}{\partial r}\, =\, \frac {\partial a}{\partial x}\,\cos \,t \,+\, \frac {\partial a}{\partial y} \,\sin \,t$ ,

$\frac {\partial a}{\partial t} \,=\, \frac {\partial a}{\partial x} \,\frac {\partial x}{\partial t} \,+\, \frac {\partial a}{\partial y} \,\frac {\partial y}{\partial t}\, =\, -r\,\frac {\partial a}{\partial x}\,\sin \,t \,+\, r\,\frac {\partial a}{\partial y} \,\cos \,t$ .

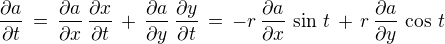Odtud vyjádříme ty parciální derivace fce "a" dle x, y.

Obdobně pro b(x,y) = Im f(x + yi) .

Výsledky pak dosadíme do CR podmínek v kartéských souřadnicích.

Ferdish · 31. 05. 2010 10:07

Diky moc, krasne to vyslo, teraz uz mozem ist pripraveny na skusku.

Matematické Fórum

#1 29. 05. 2010 23:17

Cauchy-Riemannove podmienky analyticnosti v polarnych suradniciach

#2 31. 05. 2010 09:49 — Editoval Rumburak (31. 05. 2010 10:03)

Re: Cauchy-Riemannove podmienky analyticnosti v polarnych suradniciach

#3 31. 05. 2010 10:07

Re: Cauchy-Riemannove podmienky analyticnosti v polarnych suradniciach

Zápatí