Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 31. 05. 2010 11:50
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Lineární regrese
Zdravím,
mám tady zajímavý problém, ačkoli nevím, kam bych ho zařadil, dávám to do sekce ostatní. Prošla mi rukama zajímavá publikace od Charlese Kirkpatricka, což je titul o kterém bychom dnes řekli "referenční příručka", a zaujal mně článek o regresích jako determinačním nástroji trendu. Samozřejmě, mnoho o matematickém pozadí tohoto nástroje tam napsáno není, zkoušel jsem hledat i na wikipedii, ovšem nepochopil jsem ani slovo.
Byl by někdo ochotný mi po lopatě vysvětlit postup (respektive něco-jako-vzorec) pro výpočet tím způsobem, abych pochopil sílu tohoto nástroje. V některých obchodních platformách tento nástroj mám, když ho použiju, vypadnou tři čáry, ovšem jejich úhel a orientace se mi zdá s přibývající délkou více či méně náhodná.
Prý se to k tomu používá metoda regrese nejmenších čtverců (o tom jsem na střední slyšel, ale v hlavě mi nezůstalo nic)
Přidám obrázek, na kterém se mi to snad podaří vysvětlit :) Děkuji

To jsou obrázky skutečných a aktuálních grafů forexového páru GBP/USD, první klasický OHLC, druhý čárový jenom zavírací ceny na hodinovém grafu. Nevím z čeho a jak se to počítá, radší jsem dal oba (ne všichni dokážou v candlích číst :) )
Červené čáry jsou klasické "konvenční" S/R, respektive trendline, ta regrese jsou ty tmavě modrý čáry :)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
- (téma jako vyřešené označil(a) pietro)
#2 31. 05. 2010 12:16 — Editoval BrozekP (31. 05. 2010 12:21)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Lineární regrese
↑ frank_horrigan:
Dejme tomu, že se to počítá pouze ze zavírací ceny. Když máš nějaká data (spousta dvojic  -
- 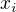 je čas a
je čas a  příslušná zavírací cena v daném čase, počet dvojic značme
příslušná zavírací cena v daném čase, počet dvojic značme  ), tak se je snažíš proložit přímkou tak, aby ta přímka co nejlépe data vystihovala. A na to se používá metoda nejmenších čtverců. Spočte se funkcionál
), tak se je snažíš proložit přímkou tak, aby ta přímka co nejlépe data vystihovala. A na to se používá metoda nejmenších čtverců. Spočte se funkcionál  (funkcionál je zde zobrazení z lineárních funkcí
(funkcionál je zde zobrazení z lineárních funkcí  do kladných reálných čísel):
do kladných reálných čísel):
 je tedy suma přes všechny dvojice. Přitom sčítáme druhou mocninu vzdálenosti skutečné hodnoty
je tedy suma přes všechny dvojice. Přitom sčítáme druhou mocninu vzdálenosti skutečné hodnoty  od hodnoty lineární funkce
od hodnoty lineární funkce  . Náš požadavek je, aby hodnoty
. Náš požadavek je, aby hodnoty  co nejlépe pro všechny body odpovídaly hodnotám
co nejlépe pro všechny body odpovídaly hodnotám  , tedy aby sčítance v sumě byly co nejmenší. A tedy chceme minimalizovat
, tedy aby sčítance v sumě byly co nejmenší. A tedy chceme minimalizovat  . Vidíme, že
. Vidíme, že  závisí pouze na parametrech lineární funkce
závisí pouze na parametrech lineární funkce  a
a  (vše ostatní známe). Budeme tedy hledat minimum funkce
(vše ostatní známe). Budeme tedy hledat minimum funkce 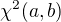 . Ze znalosti matematické analýzy víme, že derivace
. Ze znalosti matematické analýzy víme, že derivace  podle
podle  a
a  musí být v minimu nula, pokud existuje. Proto si
musí být v minimu nula, pokud existuje. Proto si  zderivujeme a položíme rovno nule.
zderivujeme a položíme rovno nule.
Teď už stačí vyřešit tuhle soustavu (to je jednoduché, stačí si to trochu rozepsat) a máme  a
a  a tedy i lineární funkci, která nejlépe aproximuje data.
a tedy i lineární funkci, která nejlépe aproximuje data.
Edit: Toto by byla ta prostřední přímka. Je ještě možné určit, jak moc dobře tato lineární funkce data aproximuje (jestli mají data velký nebo malý rozptyl okolo přímky). Předpokládám, že nějaký násobek tohoto rozptylu 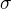 bude přičten/odečten od hodnoty b a dostaneme tak posunuté přímky:
bude přičten/odečten od hodnoty b a dostaneme tak posunuté přímky:
Offline
#3 31. 05. 2010 12:53
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Lineární regrese
Děkuji, rozhodně z tohoto vím víc než jsem věděl (to není myšleno ironicky, i když z termínů jako je derivace mi vstáváají vlasy hrůzou). Jinak, ano, máš pravdu, zkoušel jsem přes to nasadit standard deviation 1,5 a "téměř" se kryjí - nejspíš to bude nějaká forma standardní odchylky (ale jelikož se u té regrese nedá nastavit, předpokládám, že bude dynamicky podle volatity souboru. Teď se ještě naučit derivovat a používat tu regresi (přijde mi to jako sice málo známý leč silný nástroj trendové analýzy)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#4 31. 05. 2010 13:51
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Lineární regrese
↑ frank_horrigan: V praxi se nic derivovat nemusí, tím derivováním se akorát odvodí vzorec pro ty koeficienty a do něj se dosazuje:
http://cs.wikipedia.org/wiki/Line%C3%A1 … .C3.ADmkou
Lineární regrese nemusí být vždy jen aproximace přímkou, což je popsáno na téže stránce (pak by šlo vystihnout nejen že hodnota roste, ale třeba i že růst zpomaluje).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 31. 05. 2010 14:17
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Lineární regrese
↑ Kondr:
Děkuji, ten článek jsem četl a jestli něco v tom článku chápu, tak je první odstavec. Jinak, když jsem "si prohlížel obrázky", tak jsem pochopil, že ta regrese nemusí být jenom přímkou, ale i parabolou nebo nějakým vyšším polynomem, ale snažím se postupovat od toho jednoduššího, tedy lineární regrese. A že se na to ptám, když mi to umí vypočítat stroj- to je daný tím, že jsem takový "vrtal", než něco začnu používat nebo se tím aspoň zabývat, mám potřebu udělat "rozborku sborku", pak si položit otázku "k čemu mi to bude dobré" (čemuž se (v jiné souvislosti) divila kolegyňka jelena) a teprv pak jsem schopen si k nějakému nástroji vybudovat důvěru. Samozřejmě, že by se mi víc hodila regrese vyšších řádů, která je schopná postihnout sílu trendu (nerad používám věci typu MACD nebo Momentum oscillator), ovšem s mými matematickými znalostmi to je projekt na minimálně několik měsíců (nehledě na to, že se ještě učím na CMT zkoušku)
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#6 31. 05. 2010 14:36
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4247
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Lineární regrese
↑ frank_horrigan: Já jsem ho odkazoval spíše s ohledem na to, že pro koeficienty  ,
,  existují vzorce. Pokud tě zajímá "jak to funguje" tak nemusíš jít až na úroveň derivací ale stačí ti vědět, že to minimalizuje součet čtverců odchylek, tedy standardní odchylku veličiny X-A, kde X je ta náhodná funkce a A je aproximace získaná regresí. A že má cenu to používat jen tehdy, když je vysoký (v absolutní hodnotě) korelační koeficient mezi hodnotou a časem. Což z dlouhodobého hlediska v reálu není, proto jsou ty směry náhodné.
existují vzorce. Pokud tě zajímá "jak to funguje" tak nemusíš jít až na úroveň derivací ale stačí ti vědět, že to minimalizuje součet čtverců odchylek, tedy standardní odchylku veličiny X-A, kde X je ta náhodná funkce a A je aproximace získaná regresí. A že má cenu to používat jen tehdy, když je vysoký (v absolutní hodnotě) korelační koeficient mezi hodnotou a časem. Což z dlouhodobého hlediska v reálu není, proto jsou ty směry náhodné.
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#7 31. 05. 2010 14:41
Re: Lineární regrese
frank_horrigan napsal(a):
přijde mi to jako sice málo známý leč silný nástroj trendové analýzy
lineární regrese se vyučuje snad v každym základnim kurzu statistiky na libovolný VŠ. takže bych ji za málo známou nepovažoval
Offline
#8 31. 05. 2010 15:01
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: Lineární regrese
↑ Stýv:
Jo, to pravděpodobně ano (i když na VŠ jsem si nefrčel, možná příští rok, jestli se mi podaří udělat příjmačky z matiky :P :D), ale co tak jsem v kontaktu s kolegy tradery, tak to nikdo nepoužívá a málokdo ví, jak přesně to funguje (a kdo ví, nechce po lopatě říct) - z toho usuzuju jako málo známý. Já jsem na střední škole taky okolo termínu "metoda nejmenších čtverců" běžel, ale pamatuju si jenom že jsem okolo toho běžel, co jsem u toho viděl už nevím :)
↑ Kondr:
Děkuji začínám si dělat obrázek čím se to vlastně zabývám... Jinak poslední věta je asi dost podstatná a hlavně to vysvětluje proč to nikdo nechce používat. Ovšem potom vyvstává otázka, proč "klasický", tedy dotekový trendline používají všichni jak tam jsou a kdekoli na světě jsou, přičemž trpí tím samým neduhem, trend u trendujících trhů (např. velké akcie, celý $INDU, futka na cukr nebo třeba GBP/USD) trvá na tři, maxmálně 4 doteky (v lepším případě, někdy nemají ani ty dva), a tohle nechtějí používat ani jako "confirmation", případně podle toho určit aspoň slope direction (tedy vertikální směr trendu, už ne jeho úhel k času)?? Ovšem, to asi není otázka na matematiky, spíš analytiky
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#9 01. 06. 2010 10:29
Re: Lineární regrese
↑ frank_horrigan:všetko ide spočítať, záleží len na kapacite výpočtového stroja a vstupov do modelu.....to máš ako s predpoveďou počasia...je to opatrené chaosom a do troch dní Ti vedia vytvoriť dosť spolahlivé modely, vedeli by aj presnejšie, len nemajú dostatočné podklady....
Offline