Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 03. 06. 2010 16:33 — Editoval Olin (04. 06. 2010 09:58)
El. pole válce v proměnném mag. poli
Zdravím kolegy,
mám tu opět jednu úlohu na elektřinu a magnetismus.
Uvnitř dostatečně dlouhého železného kruhového válce je vytvořeno homogenní mag. pole, které má směr podél osy a rovnoměrně vzrůstá s časem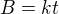 
. Průměr válce je D. Najděte intensitu el. pole ve vzdálenosti R > D/2 od osy válce.
Je jasné, že toto proměnné pole bude indukovat ve válci nějaká napětí a díky "dostatečné délce" se domnívám, že by měl jít na určení intensity el. pole použít Gaussův zákon (udělá se "plechovka" okolo válce). Ovšem nevidím, jaký mají vztah indukované veličiny jako napětí k náboji, který bych na Gaussův zákon potřeboval. Budu vděčný za každou nápovědu!
Offline
#2 03. 06. 2010 16:49 — Editoval BrozekP (03. 06. 2010 17:05)
- Pavel Brožek
- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: El. pole válce v proměnném mag. poli
Použil bych tuto Maxwellovu rovnici v integrálním tvaru. Křivka by byla kružnice o poloměru R se středem na ose. Z toho dostanu tečnou složku E, radiální dostanu nulovou z Gaussova zákona
Edit: A samozřejmě několikrát využiju symetrii.
Edit2: I když si tím nejsem úplně jistý, ještě se zamyslím. To co jsem napsal by platilo v případě nevodivého válce. Když je železný, bude to asi jinak.
Offline
#3 04. 06. 2010 10:00
Re: El. pole válce v proměnném mag. poli
Ve sbírce je bohužel jen numerický výsledek, který ale souhlasí s výsledkem po použití Maxwellovy rovnice. Takže by to asi mělo být správně.
Offline