Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 06. 2010 22:01
Sústava rovníc
V obore reálnych čísel riešte sústavu rovníc:
Ja som to riešil Gaussovou eliminačnou metódou, som zvedavý na ďaľšie napády...
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#2 07. 06. 2010 22:36
Offline
#3 07. 06. 2010 22:37
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Sústava rovníc
↑ hradecek:
Jsem si jistý, že už se tu přesně tahle soustava řešila. Ale vůbec to teď nemůžu najít :-).
Offline
#4 07. 06. 2010 22:50
- check_drummer

- Příspěvky: 5173
- Reputace: 106
Re: Sústava rovníc
Je to spíše téma k diskusi:
"Máte úhel beta." "No to nemám."
Offline
#5 07. 06. 2010 23:13
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Sústava rovníc
↑ check_drummer:
Např.
má i spoustu "nesymetrických řešení".
Offline
#6 07. 06. 2010 23:28 — Editoval FailED (08. 06. 2010 11:39)
Re: Sústava rovníc
↑ hradecek:
Je to úloha z letošní MO, A, domácí kolo. Na stránkách mají stejné řešení jako ↑ BakyX: + jedno další -link-
Neříkám že je to nejlepší postup, jen mi to při počítání přišlo jako dobrý nápad. :)
↑ check_drummer:
Bohužel to tak není, příklad:
Offline
#7 08. 06. 2010 11:22
Re: Sústava rovníc
↑ BrozekP:
Aj ja som hľadal či už sa náhodou neriešil, ale nenašiel som...
Netrápte sa nad svojimi problémami s matematikou, môžem vás uistiť, že tie moje sú ešte väčšie. ~~Albert Einstein~~
Jak spozná člověk, že není pitomec ? - Moudrý člověk to nepozná nikdy a blbci je to jedno. ~~Jak přicházejí básnici o iluze~~
Někteří lidi se nikdy nezmění. Anebo se rychle změní a pak se zase rychle změní nazpátek. ~~Homer Simpson~~
Offline
#8 08. 06. 2010 11:45
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Sústava rovníc
↑ hradecek:
Jen dodám, že můj příspěvek rozhodně nebyl myšlen jako výtka :-). Jen by v tom tématu mohly být další užitečné postupy a myšlenky.
Offline
#9 08. 06. 2010 13:48
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Sústava rovníc
↑ Marian:
Myslím, že jsi zaměnil nerovnost za obrácenou.  a
a  je splněno např. i pro
je splněno např. i pro 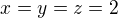 .
.
Offline
#10 08. 06. 2010 14:04
#11 08. 06. 2010 17:41
- check_drummer

- Příspěvky: 5173
- Reputace: 106
Re: Sústava rovníc
↑ BrozekP:
Zpřísněme tedy požadavky: Mějme soustavu:
f(x,y,z)=0
f(z,x,y)=0
f(y,z,x)=0
(u nás  )
)
(Pravda, nepředpokládáme zcela "symetrickou" platnost vztahů - např. f(x,z,y)=0 nepožadujeme - ale nicméně x,y,z jsou cyklicky zaměnitelné (x->y->z).)
Navíc předpokládejme, že f je ostře monotónní v každé z proměnných (tj. mimo jiné prostá), je to reálná funkce reálných proměnných, a že řešení existuje konečně mnoho (tím se vyhneme "identickým" rovnicím jako x+y+z=1,2x+2y+2z=2,3x+3y+3z=3).
Platí pak pro řešení x=y=z?
(A pokud ne, mohli bychom ještě omezit předpoklady na f, že musí obsahovat pouze polynomy, celočíselné odmocniny z polynomů a jejich lineární kombinace. Případně ještě dovolit jejich podíly.)
"Máte úhel beta." "No to nemám."
Offline
#12 08. 06. 2010 18:02
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Sústava rovníc
↑ check_drummer:
Soustava
bude mít řešení x=1, y=-1, z=0. Nejspíš bude mít soustava konečně mnoho řešení, ale neověřoval jsem to podrobněji.
Offline





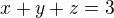

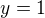
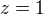
 a tedy x=1(=y=z).
a tedy x=1(=y=z). ,
,