Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 06. 2010 22:55
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
goniometrické rovnice 2.
Prosím o pomoc s příkladem, který nevím ani jak začít. Děkuji
Offline
- (téma jako vyřešené označil(a) Lucinecka88)
#2 09. 06. 2010 23:04 — Editoval zdenek1 (10. 06. 2010 13:31)
Re: goniometrické rovnice 2.
↑ Lucinecka88:




 nebo
nebo 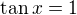
 nebo
nebo 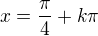
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 10. 06. 2010 11:00
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 2.
A takto to nemůžu dělat?
Offline
#4 10. 06. 2010 11:08
Re: goniometrické rovnice 2.
↑ Lucinecka88:1.,2.,3. riadok dobre 4. riadok nechápem vo4. riadku by malo byť čo treba ešte upravovať a nakoniec asi stejne prídeš na to isté čo Cheop čiže je to zložitejšie(musíš viac písať)
čo treba ešte upravovať a nakoniec asi stejne prídeš na to isté čo Cheop čiže je to zložitejšie(musíš viac písať)
MATH IS THE BEST!!!
Offline
#5 10. 06. 2010 11:27
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 2.
To máš asi pravdu, že to je složitější,ale já to nechápu a učitelka po nás vždy chtěla aby jsme to počítali přes sin a cos.
Jak jsi udělal toto?
Offline
#7 10. 06. 2010 14:37
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 2.
Mám poslední toto 
Nevím jak mám pokračovat.
↑ jarrro:
Nechapu to protože jsme nikdy nepočítali s tg a cotg. Vždy jsme too převáděli na sin a cos.
Offline
#8 10. 06. 2010 14:51 — Editoval Rumburak (11. 06. 2010 09:19)
Re: goniometrické rovnice 2.
↑ Lucinecka88:
Použijeme vzorce  ,
,  a dostaneme
a dostaneme  ,
, ,
,
zde položíme 2x = y a řešíme soustavu
 ,
,
 (toto je goniometrická identita platná pro každé y).
(toto je goniometrická identita platná pro každé y).
Offline
#9 10. 06. 2010 15:18
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 2.
můžeš mi prosím říct kde jsi vzal toto  děkuji
děkuji
Offline
#10 10. 06. 2010 15:21
#11 10. 06. 2010 20:46
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 2.
Vůbec si nevím rady, jsem totálně v prknu. Skončila jsem u  a opravdu nevím jak dál. To co jste mi poradili tak nechápu jak udělat.
a opravdu nevím jak dál. To co jste mi poradili tak nechápu jak udělat.
Offline
#12 10. 06. 2010 21:05
Re: goniometrické rovnice 2.
a co kdybys zvolila substituci? Když tedy nechceš počítat s tg a cotg, že by sis zvolila, že 
A dostala bys 
a teď by ses zase k tg vrátila:
tabulková hodnota nebo viz výše řešení od Zdeňka
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#13 11. 06. 2010 07:31 — Editoval Cheop (11. 06. 2010 08:28)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: goniometrické rovnice 2.
↑ Lucinecka88:
Substituce 

Vratka ksubstituci:
1)
2)
Aby toto platilo potom je jasné, že buď musí být obě funkce sinus i kosinus kladné nebo obě záporné. (tj. I. nebo 3. kvadrant)
potom je jasné, že buď musí být obě funkce sinus i kosinus kladné nebo obě záporné. (tj. I. nebo 3. kvadrant)
To nám dává řešení:
PS Tu tvou původní rovnici jsem umocnil na druhou a pak dále trochu poupravoval.
Nikdo není dokonalý
Offline
#14 11. 06. 2010 08:08
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 2.
Strašně moc děkuji. Hodně jsi mi pomohl.
Offline
#16 11. 06. 2010 08:28
#17 14. 06. 2010 12:04
Re: goniometrické rovnice 2.
Zkusím, Lucinečko, ještě pomalu, krok za krokem, pomocí sin x a cos x, třeba to takhle líp pochopíš:
Podmínka: 

Pomocný výpočet:

Pomocný výpočet:



Dosadím zpět do substituce:
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#18 14. 06. 2010 12:27
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 2.
↑ gadgetka:
Děkuji, pochopila jsem to.
Offline
#19 14. 06. 2010 13:36
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometrické rovnice 2.
↑ gadgetka:
při všem obdivu k úpravě a podrobnému vysvětlení a k času tomu věnovanému - postup kolegy ↑ Zdeňka: + substituce, kterou doporučuješ ↑ gadgetka: přece má lepší standardizační účinek.
Navíc použití neekvivalentních úprav vedé ke kořenům, co neplatí (myslím, že kořeny v II. a IV. kv.) - je třeba provádět zkoušku.
Je to tak? Děkuji.
↑ Lucinecka88: můj obdiv.
Offline
#20 14. 06. 2010 13:47
- Lucinecka88
- Příspěvky: 377
- Reputace: 3
Re: goniometrické rovnice 2.
↑ jelena:
Tento příklad mám vypočítany takto:
Podle výsledků to vyšlo.
Offline
#21 14. 06. 2010 14:07 — Editoval gadgetka (14. 06. 2010 14:10)
Re: goniometrické rovnice 2.
u toho áčka (u výsledků) bys měla asi uvažovat všechny kvadranty, protože řešením je  nebo ten závěr napsat jako
nebo ten závěr napsat jako 
A u béčka je to vlastně to samé, plus nezapomenout na zkoušku.
Ale vzhledem k tomu, co píše jelena a k výsledkům z učebnice, jsou zřejmě správné jen ty výsledky, které jsi ty vzala v potaz, ale nemusí tomu tak být vždycky.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#22 14. 06. 2010 15:26
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: goniometrické rovnice 2.
↑ gadgetka:
tento postup je opravdu zradný, co se tyče zápisu a následné kontroly kořenů:
pokud , tak
, tak  atd.
atd.
Myslím si, v případě tohoto zadání, tak i v případě tohoto řešení (podle mého je v pořádku, proč to předělávat na něco jiného a krkolomného?) je vhodné kolegyňce doporučit, ať se zaměří na rešení rovnic  .
.
Také si myslím, že až bude vyhlášen konkurz, kdo je největší Баба Яга, tak získám plný počet bodů a ještě mi přidaji nějaký velký bonus, děkuji :-)
Offline
 a
a a čo sa nedá chápať na Cheopovom postupe?
a čo sa nedá chápať na Cheopovom postupe? ,
,  .
.
 .
.
 tady je chyba.
tady je chyba. 
