Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 06. 2010 23:17
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
další příklady
Potřebovala bych pomoci, prosím, o jednodušší vysvětlení, vím, že je toho mnoho, ale už si nevím rady =(
1. Množina všech reálných čísel, pro která platí log při základě 11 (x^2-10x)<1 je rovna množině: výsledek (10,11)
2. Definičním oborem funkce f(x)=log(|x+1| - |4-2x|-2) je množina: výsledek (-5/3,3)
3. Množinu všech reálných čísel, pro která platí (1/6) to celé na |x-1| > 1/36. lze napsat ve tvaru:
a) (-3,1), b) (-nekonečno, -3) U (1,+nekonečno), c) (-1,3) d) (-nekonečno,-1) U (3,+nekonečno)
4. Definičním oborem funkce f(x)=1/ \sprt 2*|x+2|- 2*|3-x| -3 je množina: má to vyjít (-5/4, +nekonečno)
asi bych měla udělat nulové body, a pak?
5. Množina všech reálných čísel, pro která platí 5 na x^2-4|x|+5 >25 je rovna množině: má to vyjít
(-nekonečno,-3) U (-1,1) U (3,+nekonečno)
stále nechápu, kdy nulové body otáčím v opačné, souvisí to se znaménkama nerovnosti? když je nebo rovno tak se nemění?
6. Množina všech reálných čísel, pro která platí |7^x - 4| < 3 je rovna množině: výsledek (0,1)
7. Všechna reálná řešení rovnice 2*16^x-17.4^x + 8=0: a výsledek <-1,2>
8. Kvadratickou rovnici s reálnými koeficienty, jejíž jeden kořen má tvar x1=\sprt2 *(cos*7pí/4 + i sin 7pí/4), lze napsat ve tvaru: výsledek je x^2 -2x+2=0
Offline
- (téma jako vyřešené označil(a) jelena)
#7 12. 06. 2010 23:59
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: další příklady
↑ Mr.Pinker:
když to roznásobím vyjde mi x^2-2x+1=0
Offline
#8 13. 06. 2010 00:00
Re: další příklady
↑ lucik.kicul:
Tak ten výsledok je asi zlý. Dosadím napr. 0, čo vyhovuje "intervalu" a zistím že nenastane rovnosť
1^6 - 2^6 + 3^6 = 666
Offline
#9 13. 06. 2010 00:09
#14 13. 06. 2010 01:30
Re: další příklady
Znaménka v absolutní hodnotě otáčíš podle toho, zda vyjde výraz v absolutní hodnotě kladně či záporně. Z intervalu, který určíš podle nulových bodů, dosazuješ libovolné číslo do absolutní hodnoty, abys zjistila její kladnost či zápornost. Např.
|x-1|>0
Nulovým bodem je 1, řešíš dva intervaly  a
a 
Z prvního intervalu dosadíš do absolutní hodnoty např. 0 a zjistíš, že 0-1 je záporné číslo, takže výraz v absolutní hodnotě bude záporný, proto měníš znaménka na -x+1. Z druhého intervalu dosadíš např. 2 a dostáváš 2-1 je kladné číslo, proto je výraz v absolutní hodnotě kladný a znaménka se nemění.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#16 13. 06. 2010 07:11
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: další příklady
↑ gadgetka:
děkuju moc všem, a s tím znaménkem, co když mám nějaký příklad, kde musím zjistit nejdříve x1,x2 např. kdyby mi vyšlo x1=3 a x2= 6 proč na číselnou osu obrátím znaménka?
Offline
#17 13. 06. 2010 07:40
Re: další příklady
protože kvadratická rovnice má tvar 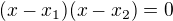 , kde x_1 a x_2 jsou kořeny kvadratické rovnice. Na číselnou osu neobracíš znaménka, nulové body jsou shodné s kořeny kvadratické rovnice...
, kde x_1 a x_2 jsou kořeny kvadratické rovnice. Na číselnou osu neobracíš znaménka, nulové body jsou shodné s kořeny kvadratické rovnice...
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#18 13. 06. 2010 08:02
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: další příklady
už je mi to jasné, a mění se znaménka na číselnou osu i kvůli = <;>, větší nebo rovno, menší nebo rovno?
Offline
#21 13. 06. 2010 10:52
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: další příklady
↑ gadgetka:
můžu se ještě zeptat na ty kořeny u příkladu 5? u (-nekonečno,0)? mě vychází u rovnice x^2+4x+3 kořeny x1= -1 a x2= -3, tak proč je tam (x+1). (x+3)? a u sjednocení je znovu -1 a -3?
Offline
#23 13. 06. 2010 11:00
- lucik.kicul
- Příspěvky: 126
- Reputace: 0
Re: další příklady
můžu tedy nechat ty kořeny, které jsem vypočítala z rovnice x1=-1 a x2=-3? nevadí to?
Offline




 nema řešení
nema řešení 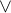





 komplexně sdružený kořen k němu je
komplexně sdružený kořen k němu je
![kopírovat do textarea $[(x-(1-i)]*[x-(1+i)]=0$](/mathtex/7a/7ad6cfce574a128ba62e47bf89fd1bcd.gif)


















