Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 18. 06. 2010 19:53
Obskúrnosť
Ahojte,
nikdy som si neuvedomil, ako môže byť aj obyčajná vec ako je guľa, taká obskúrnosť. Nie, že by mala byť zaujímavá trojrozmerná guľa, ale hlavne čo sa týka gúľ vo vyšších rozmeroch. Pomerne známy vzťah pre výpočet objemu n-rozmernej gule nám poskytne akú takú predstavu. Keď skúmame vlastnosti n-rozmernej kocky a gule do nej vpísanej, dospejem k zaujímavým záverom. Pomer ich objemov je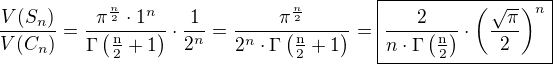
Pričom som vzal kocku so stranou dĺžky 2 a polomer gule do nej vpísanej bude 1. Keďže sa zaoberám veľkými rozmermi, zúžim ich na párne n (pre účely gama)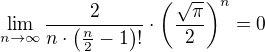
Konvergencia je veľmi rýchla. Už pre n = 6 máme pomer približne 0.0807 Naskytajú sa prirodzené otázky. Možno mám skreslenú predstavu o vpísaných guliach v rozmeroch vyšších ako 3. Vôbec totiž netuším, či polomer gule vpísanej do kocky je nutne polovica dĺžky hrany tejto kocky. Analógia sa dá vyvodiť z nižších rozmerov, no ktovie.
V podstate, čím vyšší máme rozmer, tým je gulička menšia. Deformuje sa nejako čudne. Keďže si to predstaviť nijako neviem, spravil som analógiu pre 2D. Predstavujem si to aj nejako takto
No, je to zrejme mylná predstava, ale nedá sa to. Zvláštne, že?
"The mathematical rules of the universe are visible to men in the form of beauty."
John Michel
Offline
- (téma jako vyřešené označil(a) lukaszh)
#2 18. 06. 2010 20:41
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Obskúrnosť
Když budu mít hyperkouli danou rovnicí
a budu hledat tečnou nadrovinu  , tak jedině nadroviny
, tak jedině nadroviny 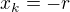 a
a 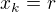 budou mít s hranicí hyperkoule společný právě jeden bod. Takže bych řekl, že rozměr hyperkrychle by opravdu měl být 2r.
budou mít s hranicí hyperkoule společný právě jeden bod. Takže bych řekl, že rozměr hyperkrychle by opravdu měl být 2r.
Edit: Obrázku nerozumím.
Offline
#3 18. 06. 2010 21:13
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Obskúrnosť
Jo, poloměr je správně. A dokonce ta koule bude stále konvexní, ne jako na obrázku. Stačí si uvědomit, že pro zobecněný osmistěn, který se krychle dotýká ve stejných bodech jako koule, bude ten poměr  , což jde k nule ještě o chlup rychleji.
, což jde k nule ještě o chlup rychleji.
To, že koule s větší dimenzí "zmenšují objem" je trochu neintuitivní, ale má to celkem pozitivní důsledky v teorii kódování (viz Sphere packing bound, a.k.a Hamming bound).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
